Area of a regular polygon
The area of a regular polygon (also called n-gon) can be derived with some basic knowledge of geometry and trigonometry. We will show you how to derive 3 formulas that you can use to get the area of an n-gon.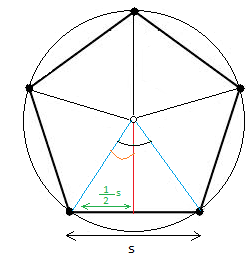
Our strategy before we derive the formula of the area of a regular polygon will be to show you how to get the area of a pentagon and then generalize the approach for an n-gon
To get the area of the pentagon above, follow the steps below:
1. Break the pentagon into 5 congruent triangles
2. Get the area for one triangle
3. Multiply by 5 to get the area for all 5 triangles or the whole pentagon
Notice that the pentagon has 5 sides and you can make 5 triangles. Similarly, the n-gon has n sides and you can make n triangles.
The formula to get the area of a triangle is A =
base × height
2
Looking at the triangle above, you can see that the base is s and s is also the length of one side of the pentagon. The red line is the height and it is called apothem in an n-gon
Say that s = 4 and apothem = 8
A =
4 × 8
2
Since there are 5 triangles in a pentagon A = 5 ×
4 × 8
2
First generalization of the area of a regular polygon
base = s and height = apothem. An n-gon has n triangles
Since there are n triangles in an n-gon, A = n ×
s × apothem
2
Sometimes, s is not given, but you know the apothem and the number of sides. So you need to find s in this case. You will need some basic trigonometric identities
You need to know also how to get the central angle. Take a look at the figure again, the central angle is the one in black
Find the area when n = 5 and apothem = 8
Call the angle in orange x and use trigonometric identity.
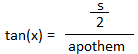 |
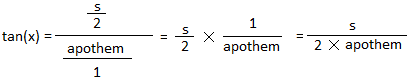 |
tan (x) =
s
2 × 8
tan (x) =
s
16
If 4 =
8
2
then, 8 = 4 × 2
Similarly, if tan(x) =
s
16
then, s = tan(x) × 16
Now, we have to find x. x is half the angle in black. The angle in black is the central angle.
The central angle can be found by using the formula: Central angle =
360 degrees
n
n is the number of sides.
Central angle =
360 degrees
5
= 72 degrees
The angle in orange or x is equal to 72 divided by 2 or 36 degrees. Thus, s = tan(36°) × 16
Putting it all together, A = 5 ×
tan(36°) × 16 × 8
2
This math can be done fairly easily, but we will not do it so you can better see how we can generalize and come up with a formula for an n-gon
Second generalization of the area of a regular polygon
base = s , height = apothem and the n-gon has n sides
A = n ×
s × apothem
2
Using tan(x) =
s
2 × apothem
, we get s = tan(x) × 2 × apothem
Find x for an n-gon.
Central angle =
360 degrees
n
Recall though that x is the orange angle, so
360 degrees
n
must be divided by 2
This gives x =
180 degrees
n
s = tan(
180 degrees
n
)× 2 × apothem
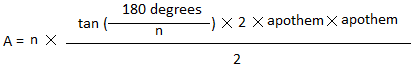 |
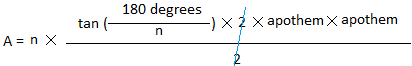 |
|
|
|
|
Derivation of the area of a regular polygon when s and n are given, but the apothem is not known
Since the apothem is missing we can use the formula s = tan(x) × 2 × apothem and solve for apothem.
Replace the apothem into the formula for the area and simplify. You will end up with an equation in terms of s and the angle
s = 2 × tan(x) × apothem
apothem =
s
2 tan(x)
A =
s
2 tan(x)
If we rewrite A = n ×
s × apothem
2
it will be easier to manage
A =
n × s
2
× apothem
|
A =
n × s
2
×
|
s
2 × tan(x)
|
A =
n × s2
4 × tan(x)
x is still the same angle, so x =
180 degrees
n
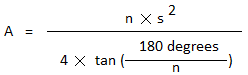 |
Derivation of the area of a regular polygon when the radius is given, but the apothem and s are not known
The radius is the blue line or the hypotenuse. If x is the angle in orange and let the radius be r we get:
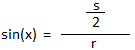 |
sin(x) =
s
2 × r
s = 2 × r sin(x)
cos(x) =
apothem
r
apothem = cos(x) × r
Replace the value for the apothem and s into the formula A = n ×
s × apothem
2
A = n ×
2 × r sin(x) × cos(x) × r
2
A = n ×
2 × sin(x) × cos(x) × r2
2
Useful trigonometric formula: sin(2x) = 2 sin(x)cos(x)
A = n ×
sin(2x) × r2
2
x =
180 degrees
2
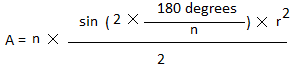 |
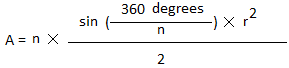 |