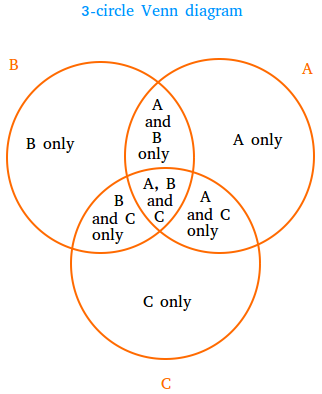
3 Circle Venn Diagram

Definition

A 3 circle Venn diagram, named after the English logician John Venn, is a diagram that shows how the elements of three sets are related using three overlapping circles.

When the three circles in a Venn diagram overlap, the overlapping parts contain elements that are common to any two circles or all the three circles.

In this lesson, you will learn

  • What each part of a 3 circle Venn diagram means
  • The difference between "A and B" and "A and B only"
  • How to put the elements of three sets into a Venn diagram

How to Understand the Overlaps in a 3 Circle Venn Diagram

Let’s consider three sets A, B, and C and their corresponding circles:

  • Set A: Students who play ping pong.
  • Set B: Students who play soccer.
  • Set C: Students who play basketball.
3 circle Venn diagram with circles A, B and C and the regions A only, B only, C only, A and B only, B and C only, A and C only, and A, B and C in the middle

Non-Overlapping Sections

These represent elements that are unique to just one set. For example, students who only play ping pong would fall into the non-overlapping part of circle A.

Two-Circle Overlaps

These represent elements that are common to two sets but not the third set. For example, the overlap between circles A and B would represent students who play both ping pong and soccer but not basketball.

Three-Circle Overlap

These represent elements common to all three sets. In our example, this would be students who play ping pong, soccer, and basketball.

Rule

Some important observations:

  • Elements in A and B = elements in A and B only plus elements in A, B, and C.
  • Elements in B and C = elements in B and C only plus elements in A, B, and C.
  • Elements in A and C = elements in A and C only plus elements in A, B, and C.
Common mistake

Forgetting the middle when counting a two-circle overlap. If 3 students play ping pong and soccer only, and 2 students play all three sports, then 3 + 2 = 5 students play both ping pong and soccer, not 3.

A student plays soccer and basketball but not ping pong. Which part of the diagram is this student in?

Show answer

B and C only. The student is in circle B and circle C but not in circle A, so the student goes in the overlap of B and C, outside A.

Example Showing How to Create a 3 Circle Venn Diagram

We can create a 3-circle Venn diagram to show the relationships between the factors of 30, 40, and 100.

  • Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
  • Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
  • Factors of 100: 1, 2, 4, 5, 10, 20, 25, 50, 100
3 circle Venn diagram of the factors of 30, 40 and 100: 1, 2, 5 and 10 in the middle, 4 and 20 in the overlap of 40 and 100 only, 3, 6, 15 and 30 in 30 only, 8 and 40 in 40 only, and 25, 50 and 100 in 100 only

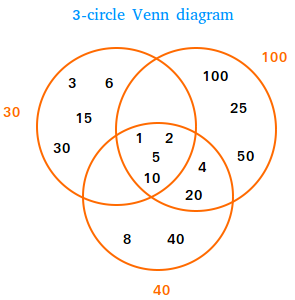
Non-Overlapping Sections

  • Factors of 30: 3, 6, 15, 30
  • Factors of 40: 8, 40
  • Factors of 100: 25, 50, 100

Two-Circle Overlaps

  • Factors of 30 ∩ Factors of 40 only: { }
  • Factors of 30 ∩ Factors of 100 only: { }
  • Factors of 40 ∩ Factors of 100 only: {4, 20}

Three-Circle Overlaps

  • Factors of 30 ∩ Factors of 40 ∩ Factors of 100: {1, 2, 5, 10}

In the factors diagram, why is 20 in the overlap of the 40 and 100 circles only?

Show answer

20 is a factor of 40 and 100, but not of 30. 40 ÷ 20 = 2 and 100 ÷ 20 = 5, but 30 ÷ 20 is not a whole number.

How to Fill In a 3 Circle Venn Diagram

Start in the middle and work outward. Each element goes in exactly one part of the diagram.

Worked example: Draw a 3 circle Venn diagram for A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7} and C = {5, 7, 8, 9}.
  1. Middle (A, B and C): only 5 is in all three sets, so write 5 in the middle.
  2. A and B only: 4 is in A and B but not in C.
  3. B and C only: 7 is in B and C but not in A.
  4. A and C only: no number is in A and C without also being in B, so this part is empty.
  5. One circle only: A only is {1, 2, 3}, B only is {6} and C only is {8, 9}.
  6. Check: every element of A, B and C appears exactly once in the diagram.

Middle {5}, A and B only {4}, B and C only {7}, A and C only { }, A only {1, 2, 3}, B only {6}, C only {8, 9}.

In the worked example, how many elements are in both A and B?

Show answer

2. A and B only has 1 element (4), and the middle has 1 element (5), so 1 + 1 = 2.

Summary

  • A 3 circle Venn diagram uses three overlapping circles to show how three sets are related.
  • It has 7 parts inside the circles: 3 one-circle parts, 3 two-circle overlaps and the middle.
  • A two-circle overlap shows elements in those two sets but not the third.
  • The middle shows elements in all three sets.
  • Elements in A and B = elements in A and B only plus elements in A, B, and C.
  • To fill in a diagram, start in the middle and put each element in exactly one part.

Test Yourself: 10-Question Quiz

Now check what you learned. Every answer is explained, and each time you play you get new questions.

Question 1 of 10Score: 0

Keep learning