Adding vectors
Adding vectors to find the resultant is an important skill in mathematics and also physics. Therefore, understanding the concept is important to do well in physics or mathematics.
Let's say you are pushing your friend and it requires an effort of 100 pounds.
Your friend is not as strong as you are, so he is applying a force of 50 pounds.
We illustrate this situation with the two vectors above.
You are the blue vector and your friend is the green vector. Both vectors look like rays. Indeed, a vector is a directed line segment.
The little dot is called tail or initial point and the arrow is called head or terminal point.
I purposely made the blue vector twice as big as the green one.
Do you know why? It is because the force you are applying is twice as big as your friend.
Both vectors give you two quantities. These quantities are the force and the directions.
You already know what the force is for you and your friend. Now you can clearly see that the direction of the force is toward the other person.
Many quantities in real life will require both magnitude and the direction. We call these quantities vector quantities.
When quantities can only be specified by their magnitude, we call then scalar.
For example, 20 kg of sugar going east make no sense since we don't need to know the direction at all.
It makes sense then to specify 20 kg of sugar only with the magnitude that is 20 kg.
However, driving east on the highway with a speed of 60 miles per hour makes perfect sense.
It is a vector quantity with a magnitude of 60 miles per hour and a direction of east.
Adding vectors to find the resultant
What is the resultant of you pushing your friend and your friend pushing you? It may make sense to you that since your force is stronger, your friend will move in the same direction that you are moving.
The net force you will be moving him with is 50 pounds.
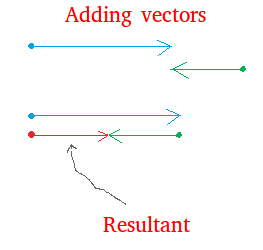
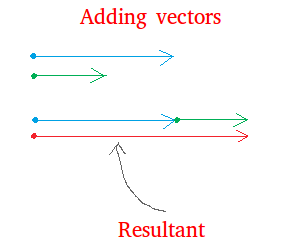
If you and your friend join forces to push a car, notice this time that
both arrows are pointing in the same direction. The force is now bigger
and it is 150 pounds.
Adding vectors when the directed segments are not parallel
Adding vectors when the directed segments are not parallel is not very much different than when they are parallel.
You may have noticed that the initial point of the vector in green was always put at the terminal point of the vector in blue. The resultant has the same initial point as the vector in blue and the same terminal point as the vector in green.
We do the same thing when the vectors are not parallel. For example, add the following vectors:
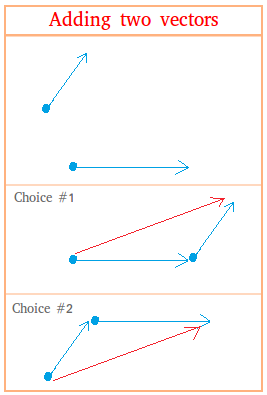
Notice that in choice #1, we put the initial point of the smaller vector at the terminal point of the bigger vector. In choice #2, we put the initial point of the bigger vector at the terminal point of the smaller vector.
You could also use the parallelogram rule to add the two vectors above.
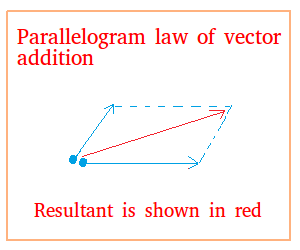
In the parallelogram rule, notice that the initial points of the vectors are put next to each other.
How to subtract vectors
Subtracting vectors is just like adding vectors. Say you want to do
A - B
A - B = A + -B
-B is the opposite of B. Both vectors have the same length, but they have opposite directions.
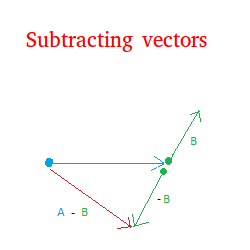
The figure below shows A - B.
A is the blue vector. B is the green vector pointing upward.
The vector pointing downward is the opposite of B.
A - B is the resultant vector shown in red.
Adding vectors quiz
This vector addition quiz will help you determine if you know how to do vector addition. You will not need to use a paper and pencil to complete this quiz.
First, read the lesson about adding vector and then take this quiz.
Objective of the quiz:
- know what a resultant is.
- Learn how to find the resultant.
- Identify tail and head of a vector.
- Find the resultant for real life situations