Angle bisector theorem

The angle bisector theorem states the following: If a point is on the bisector of an angle, then the point is equidistant from the sides of the angle. For example, take a look at the angle below shown with two blue rays.

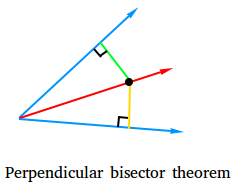
The red line is the perpendicular bisector and the black point is on the perpendicular bisector. Since the black point is on the perpendicular bisector, the black point is equidistant from the sides of the angle.

We illustrate this fact with the green and yellow segment. The length of the green segment is the same as the length of the yellow segment.

Using the angle bisector theorem to solve a geometry problem.

Take a look at the diagram below and find the length of segment CD.

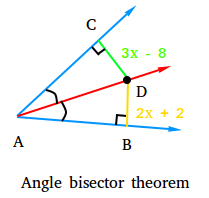
From the diagram, you can see that D is on the bisector of angle CAB.

Therefore, DC = DB

3x - 8 = 2x + 2

3x -2x - 8 = 2x - 2x + 2

3x - 2x - 8 = 0 + 2

x - 8 = 2

x - 8 + 8 = 2 + 8

x + 0 = 10

x = 10

CD = 3x - 8 = 3(10) - 8 = 30 - 8 = 22