Find the centripetal acceleration 

The formula to find the centripetal acceleration is the following. In this lesson, we will show you how to derive the formula and solve a little problem.

We start by showing an object that moves a tiny distance from point A to point B. 

The speed of the object at point A is v₁ and the speed of the object at point B is v₂. Keep in mind though that this is a uniform circular motion, so the speed is constant. In other words, v₁ = v₂.

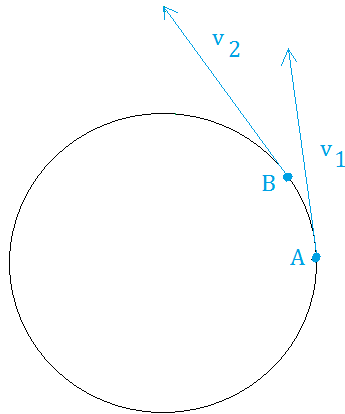
The only thing that changed is the direction.

Now, ask yourself,"By how much did the object move from point A to point B? "

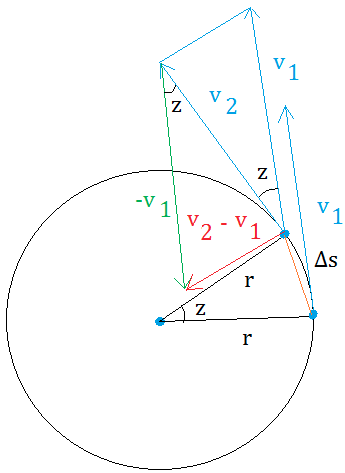
You will need to draw the radii from the center of the circle to point A and point B.                                                 

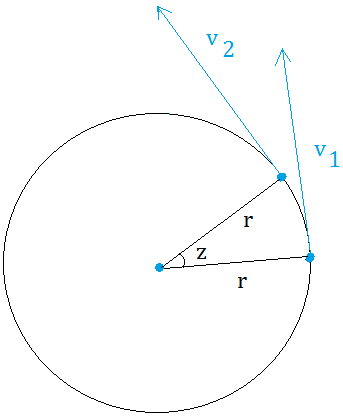
From point A to point B, the object moved by a tiny distance represented by angle z. Since we are looking for the acceleration, we will need to write formulas for acceleration and for the speed. First, let us find the speed or v

Between point A and point B, Δs is the distance the object traveled. Δs is the small arc between A and B. Try to picture in your mind the angle z being very small. In this case, both the orange line and the arc will get very small. Moreover, when the arc is very small, it will coincide with the orange line and be the same as the orange line. (When an arc is very small, it looks like a straight line)

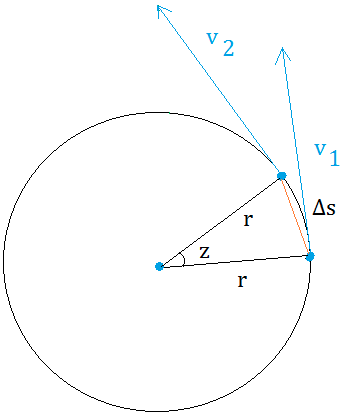
Therefore, when z is very small, the orange line is also equal Δs or s₂ -s₁.


Multiply both sides by Δt. We get Δs = v Δt

Now what about the acceleration?


Δv = v₂ - v₁. We need to graph v₂ - v₁ before we can derive the formula for centripetal acceleration.

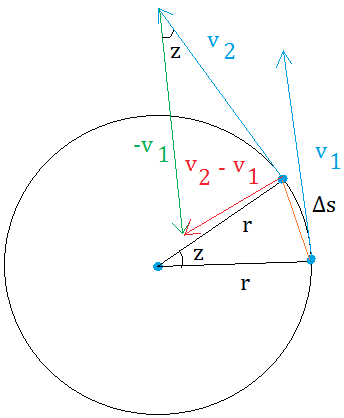
Now, you can see two triangles.  Did you make these observations?

• Between -v1 and v2, the angle is also z. Take a look at the parallelogram in the figure below to see why this make sense.
  
  
• v2 - v1 is directed toward the center. Therefore, the acceleration will also be directed toward the center.
  
  
• The two triangles are similar by SAS. 
  
  
• v2 = v1  = v

Since the triangles are similar, we can form the following proportion.

Replace Δs with v Δt



Multiply both sides by v

In the figure below, we moved v1 up and to the left by putting its tail next to the tail of v2. We just need to make sure that we don't change the angle. The angle will then still be z.

Finally, change the direction of v1 an put its tail at the head of v2. This gives a parallelogram.

In this parallelogram z and z are alternate interior angles and alternate interior angles are always equal.

A centripetal acceleration exercise

A car moves around a circle of radius 50 meters with a speed of 25 m/s. What is the centripetal acceleration?