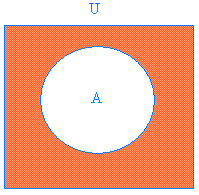
Complement of a set

This lesson will explain how to find the complement of a set. We will start with a definition.

Given a set A, the complement of A is the set of all element in the universal set U, but not in A. We can write A^c. You can also say complement of A in U.

Example #1.

Take a close look at the figure above. d and f are in U, but they are not in A.

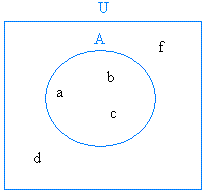
Therefore A^c = {d, f}

Sometimes, instead of looking at a the Venn Diagrams, it may be easier to write down the elements of both sets

Then, we show in bold the elements that are in U, but not in A

A = { a, b, c}

U = { a, b, c, d, f}


Example #2.


Let B = {1 orange, 1 pineapple, 1 banana, 1 apple}

Let U = {1 orange, 1 apricot, 1 pineapple, 1 banana, 1 mango, 1 apple, 1 kiwifruit }

Again, we show in bold all elements in U, but not in B

B^c = {1 apricot, 1 mango, 1 kiwifruit}


Example #3.


Find the complement of B in U

B = { 1, 2, 4, 6}

U = {1, 2, 4, 6, 7, 8, 9 }

Complement of B in U = { 7, 8, 9}


Example #4.


Find the complement of A in U

A = { x / x is a number bigger than 4 and smaller than 8}

U = { x / x is a positive number smaller than 7}

A = { 5, 6, 7} and U = { 1, 2, 3, 4, 5, 6}

A^c = { 1, 2, 3, 4}

Or A^c = { x / x is a number bigger than 1 and smaller than 5 }

The graph below shows the shaded region for the complement of set A

Complement of a set quiz. Take the quiz to see how well you understand this lesson.