Conditional statement

A conditional statement or simply conditional is an if-then statement such as this one: If you are not completely satisfied with your purchase, then you can return the product and get a full refund.

The symbol that we use to represent an if-then statement is p → q

We read p → q  as "if p then q" or "p implies q"

A conditional statement has an hypothesis and a conclusion. The hypothesis is the part p following if and the conclusion is the part q following then.

Identifying the hypothesis and the conclusion of a conditional statement

Example #1 :

Identify p and q for this conditional: If you are not completely satisfied with your purchase, then you can return the product and get a full refund.

Hypothesis or part p : You are not completely satisfied with your purchase.

Conclusion or part q : You can return the product and get a full refund.

Example #2 :

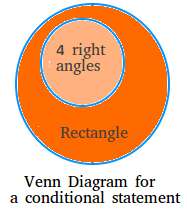
If a quadrilateral has four right angles, then it is a rectangle.

Hypothesis : a quadrilateral has four right angles.

Conclusion : it is a rectangle.

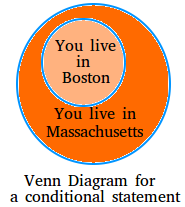
Using a Venn Diagram to identify parts of a conditional statement

The set of things that satisfy the hypothesis lies inside the set of things that satisfy the conclusion. In the Venn Diagram below, notice how p or the hypothesis lies completely inside the conclusion or q.

The diagram below illustrates this conditional : If you live in Boston, then you live in Massachusetts. And of course, other conditions can go inside the big circle

Here is another example illustrating how a hypothesis is contained within a conclusion. This is the Venn Diagram for example #2 mentioned before.