Discriminant of a quadratic equation
The discriminant of a quadratic equation in the form ax2 + bx + c = 0 is the value of the expression b2 - 4ac.

The value of the discriminant determines if the quadratic equation has real or complex numbers solutions.
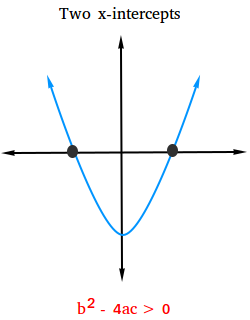
Case #1:
The value of the discriminant is bigger than 0: b2 - 4ac > 0
If the value of the discriminant is bigger than 0, then the quadratic equation has two real solutions and the graph of the related function has two x-intercepts.
The x-intercepts of f(x) = ax2 + bx + c are the solutions of ax2 + bx + c = 0.
The figure below shows what the graph looks like with two x-intercepts.
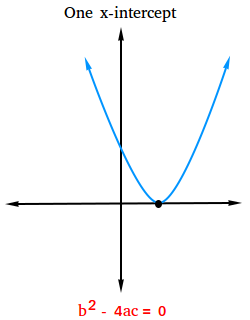
Case #2:
The value of the discriminant is equal to 0: b2 - 4ac = 0
If the value of the discriminant is equal to 0, then the quadratic equation has one real solution and the graph of the related function has one x-intercept.
The x-intercepts of f(x) = ax2 + bx + c are the solutions of ax2 + bx + c = 0.
The figure below shows what the graph looks like with one x-intercept.
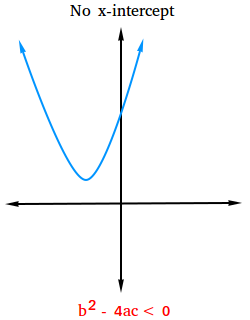
Case #3:
The value of the discriminant is smaller than 0: b2 - 4ac < 0
If the value of the discriminant is smaller than 0, then the quadratic equation has no real solution, but two imaginary solutions instead. The graph of the related function has no x-intercept.
The figure below shows what the graph looks like with no x-intercept.