Electric field problems

The following electric field problems will help you sharpen your knowledge of electric field. Things that you absolutely need in order to solve the problems on this lesson.

• Know how to use the formula below:

• Know how to draw the electric field vector.

• Know how do solve math problems that have multiplication and division of exponents.

• Use k = 9 × 10⁹ N.m²/C₂

• Convert d to meter before doing the math.

• The electric field unit is N/C

Problem #1

A particle with charge q = 5Q is placed at a distance d from a point A.

1. Calculate the electric field produced at the point A in terms of k, Q and d.

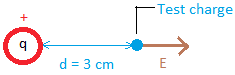
2. Calculate the electric field produced at the point A if Q = 10^-10 and d = 3 cm.

Solution

When solving electric field problems, you need to find the magnitude and the direction of the electric field. You cannot just look for one and forget about the other.

To find the magnitude, use the formula shown above.

To find the direction, put a small positive test charge in the field and then find out if it will be attracted or repulsed.

For this problem it is very easy to find the magnitude of the electric field. Just substitute 5Q for q. The next two electric field problems will take things to the next level.

1.

2.
d = 3 × 10^-2

d² = 9 × 10^-4





E = 5 × 10³ N/C

Put the test charge at point A. The direction of the electric field is shown below. 

More challenging electric field problems

Problem #2

Two particles with charges q₁ = 4Q and q₂ = -8Q are placed at the same distance d from a point A. Charges q₁ and q₂ and point A are all on the same line. Calculate the electric field produced at the point A in terms of k, Q and d.

Let E₁ be the electric field for q₁
Let E₂ be the electric field for q₂


Net electric field = E = E₁ + E₂

Since the denominator is the same, we can just add 4Q and 8Q.

4Q + 8Q = 12Q

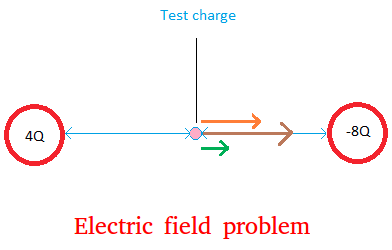
Put the test charge at point A. The direction of the electric field is shown below with the brown arrow.

Notice how the brown vector is the result of adding the green vector and the orange vector.

Notice also how the size of the orange vector is twice that of the green since 8Q is twice 4Q.

Problem #3

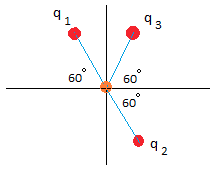
Three particles with charges q₁ = 2Q, q₂ = -2Q, and q₃ = 4Q are placed at the same distance d from a test charge placed at the origin. Charges q₁ , q₂, and q₃ and point A are arranged as you see below. Calculate the electric field produced at the point A in terms of k, Q and d. q₁ is positive, so the orange test charge is repulsed by q₁. We show this with the first brown arrow

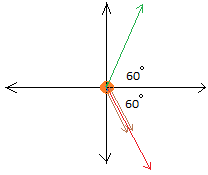
q₂ is negative, so the orange test charge is attracted to q₂. We show this with the second brown arrow.





Let E₃ be the electric field for q₃ (Shown with green arrow)

We need to find the net electric charge for E₃ (Green arrow) and E₁ and E₃ (Red arrow)

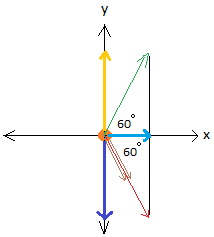
We need to add all the x components and all the y components for the two vectors (green  and red).

When looking at the graph, I see that the y components are shown in gold and dark blue. Moreover,  I immediately see that the y components add up to zero.

For both the green and the red vector, the x components is the blue line.

Find the x component of the green vector

Line in blue = line in green × cos(60°)

Line in blue = line in green × 0.5

To Find the x component of the red vector, we basically repeat what we did for the green vector to end up with the exact same answer.

Perhaps the last two electric field problems were hard. Send your questions.