Even and Odd Numbers
Integers consist of even and odd numbers. The set of integers = {..., -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ...}
The set of even numbers = {... ,-8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ...}
The set of odd numbers = {... ,-9, -7, -5, -3, -1, 1, 3, 5, 7, 9, ...}
From the list above, we can make the following conclusions:
- The smallest even number is not zero since there are plenty of other even numbers that are negative and smaller than zero such as -4 and -8.
- The smallest positive even number is 2.
- The smallest positive odd number is 1.
- The only even prime number is 2.
What are even numbers? Definition and examples
An even number is any number that gives a remainder of zero when divided by 2. For example, 12 gives a remainder of 0 when divided by 2, so 12 is even.
You can also say that 12 is even because there exist a number 6, such that 12 = 2 × 6. Having said that, we can come up with a formal definition.
Formal definition of an even number:
A number n is even if there exist a number k, such that n = 2k, where k is an integer.
2k, where k is an integer is the general form of an even number
This is the formal way of saying that if n is divided by 2, we always get a quotient k with no remainder. This means that n can in fact be divided by 2.
How to quickly check if a given number is even?
We saw in divisibility rules that a number is divisible by 2 or gives a remainder of zero if its last digit is 0,2,4,6,or 8.
Therefore, any number whose last digit is 0, 2, 4, 6, or 8 is an even number. For example, 98716 is an even number because its last digit shown in red is 6.
Other examples of even numbers are 58, 44884, 998632, 98, 48, and 10000000.
Another way to quickly check if a number is even is to see if you can make two equal parts with the number. For example, 50 is even since I can make two equal parts with 50 (25 and 25)
What are odd numbers? Definition and examples
An odd number is any number that gives a remainder of 1 when divided by 2. For example, 27 gives a remainder of 1 when divided by 2, so 27 is odd.
You can also say that 27 is odd because there exist a number 13, such that 27 = 2 × 13 + 1. Having said that, we can come up with a formal definition.
Formal definition of an odd number:
A number n is odd if there exist a number k, such that n = 2k + 1 where k is an integer.
2k + 1, where k is an integer is the general form of an odd number
This is the formal way of saying that if n is divided by 2, we always get a quotient k with a remainder of 1. This means that n cannot in fact be divided by 2.
How to quickly check if a given number is odd?
Again, we saw in divisibility rules that a number is divisible by 2 or gives a remainder of zero if its last digit is 0,2,4,6,or 8.
Therefore, any number whose last digit is not 0, 2, 4, 6, or 8 is an odd number.
Other examples of odd numbers are 53, 881, 238637, 99, 45, and 100000023
Even and Odd Numbers (1-200)
Even Numbers (2-200)
| Even Numbers | ||||
|---|---|---|---|---|
| 2 | 4 | 6 | 8 | 10 |
| 12 | 14 | 16 | 18 | 20 |
| 22 | 24 | 26 | 28 | 30 |
| 32 | 34 | 36 | 38 | 40 |
| 42 | 44 | 46 | 48 | 50 |
| 52 | 54 | 56 | 58 | 60 |
| 62 | 64 | 66 | 68 | 70 |
| 72 | 74 | 76 | 78 | 80 |
| 82 | 84 | 86 | 88 | 90 |
| 92 | 94 | 96 | 98 | 100 |
| 102 | 104 | 106 | 108 | 110 |
| 112 | 114 | 116 | 118 | 120 |
| 122 | 124 | 126 | 128 | 130 |
| 132 | 134 | 136 | 138 | 140 |
| 142 | 144 | 146 | 148 | 150 |
| 152 | 154 | 156 | 158 | 160 |
| 162 | 164 | 166 | 168 | 170 |
| 172 | 174 | 176 | 178 | 180 |
| 182 | 184 | 186 | 188 | 190 |
| 192 | 194 | 196 | 198 | 200 |
Odd Numbers (1-199)
| Odd Numbers | ||||
|---|---|---|---|---|
| 1 | 3 | 5 | 7 | 9 |
| 11 | 13 | 15 | 17 | 19 |
| 21 | 23 | 25 | 27 | 29 |
| 31 | 33 | 35 | 37 | 39 |
| 41 | 43 | 45 | 47 | 49 |
| 51 | 53 | 55 | 57 | 59 |
| 61 | 63 | 65 | 67 | 69 |
| 71 | 73 | 75 | 77 | 79 |
| 81 | 83 | 85 | 87 | 89 |
| 91 | 93 | 95 | 97 | 99 |
| 101 | 103 | 105 | 107 | 109 |
| 111 | 113 | 115 | 117 | 119 |
| 121 | 123 | 125 | 127 | 129 |
| 131 | 133 | 135 | 137 | 139 |
| 141 | 143 | 145 | 147 | 149 |
| 151 | 153 | 155 | 157 | 159 |
| 161 | 163 | 165 | 167 | 169 |
| 171 | 173 | 175 | 177 | 179 |
| 181 | 183 | 185 | 187 | 189 |
| 191 | 193 | 195 | 197 | 199 |
The figure below shows the difference between even and odd numbers.
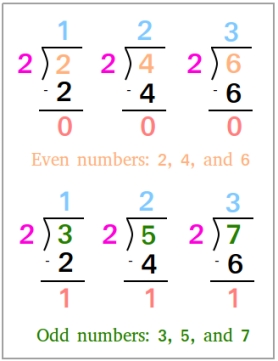
In mathematics, the parity of an integer is either even or odd. For example, the parity of 22 is even while the parity of 23 is odd. 25 and 27 have the same parity.
Important properties of even numbers and odd numbers
Property of addition
Adding two even numbers
The sum of two even numbers is an even number.
even + even = even
4 + 2 = 6
Generally speaking, let n1 = 2k1 be an even number and let n2 = 2k2 be another even number.
n1 + n2 = 2k1 + 2k2
n1 + n2 = 2(k1 + k2)
Notice that any number multiplied by 2 is even. This is the reason that 2(k1 + k2) is an even number!
Adding an even number to an odd number
The sum of an even number and an odd number is an odd number.
even + odd = odd
6 + 3 = 9
Generally speaking, let n1 = 2k1 be an even number and let n2 = 2k2 + 1 be an odd number.
n1 + n2 = 2k1 + 2k2 + 1
n1 + n2 = 2(k1 + k2) + 1
Adding two odd numbers
The sum of two odd numbers is an even number.
odd + odd = even
13 + 13 = 26
Generally speaking, let n1 = 2k1 + 1 be an odd number and let n2 = 2k2 + 1 be another odd number.
n1 + n2 = 2k1 + 1 + 2k2 + 1
n1 + n2 = 2(k1 + k2) + 2
Notice that 2(k1 + k2) is even and 2 is even.
Therefore, 2(k1 + k2) + 2 is even since adding two even numbers is equal to an even number
Property of multiplication
The product of two even numbers is an even number.
even × even = even
2 × 6 = 12
The product of an even number and an odd number is an even number.
even × odd = even
8 × 3 = 24
The product of two odd numbers is an odd number.
odd × odd = odd
3 × 5 = 15
Property of subtraction
The difference of two even numbers is an even number.
even − even = even
8 − 4 = 4
The difference of an even number and an odd number is an odd number.
even − odd = odd
6 − 3 = 3
The difference of two odd numbers is an even number.
odd − odd = even
13 − 3 = 10
If you did not fully understand this lesson about even and odd numbers, just contact me.