Factoring algebraic expressions

Factoring algebraic expressions require a solid understanding of how to get the greatest common factor (GCF)

I will not repeat the whole process here. Therefore, go here and review how to get the GCF before you start studying this lesson.

Basically, when factoring algebraic expressions, you will first look for the GCF and use your GCF to make your polynomial look like a multiplication problem:

GCF times(                         )                or          GCF times(             Blank             )

where blank is a polynomial with the same amount of term as the original polynomial.

Recall that terms are separated by addition signs, never by multiplication sign.

A few examples about factoring algebraic expressions

Example #1:

Factor x²y⁴ + 2x²

This expression has two terms. The first term is x²y⁴ and the second is 2x²

What you see in bold is the GCF:x²                            x²y⁴ + 2x²

So, we are going to make x²y⁴ + 2x² look like:

x² times (                         )

Now you need to fill in the blank as shown below:

So, your first term is whatever you multiply x² to get x²y⁴.

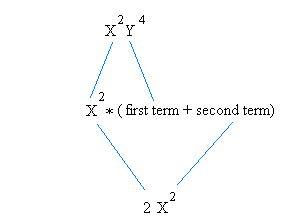
And whatever you multiply x² to get 2x² is your second term.

Therefore, x²y⁴ + 2x² = x²(y⁴ + 2)

There is an easier way to solve the problem

x²y⁴ + 2x²

Still do x² times (                         )

Then, in the expression x²y⁴ + 2x², take a pencil and cross out or erase the GCF x².Then, whatever is left is your first and second term.

Another example

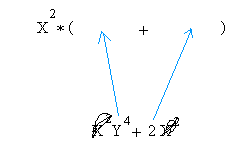
2)

8Y³B² + 16Y²B

Rewrite the expression as: 8 × Y² × Y × B × B + 8 × 2Y²B

Everything in bold is the GCF 8 × Y² × Y × B × B + 8 × 2Y²B

The GCF is 8Y²B. The answer looks like 8Y²B × (                         )

In the expression 8 × Y² × Y × B ×B + 8 × 2Y²B, erase the GCF. Whatever is left is your first and second term.

The answer is 8 × Y² × Y × B × B + 8 × 2Y²B = 8Y²B × (YB + 2)

3)

If instead you were factoring 8Y³B² − 16Y²B, you will do the same thing with the exception that there will be a minus sign between the two terms. That is all!

8Y³B² − 16Y²B = 8Y²B × (YB − 2)

4)

Factor 5(x-2) + 6x(x-2) Everything in bold is your GCF 5(x-2) + 6x(x-2)

So, (x-2) × ( 5 + 6x)