Finding the greatest common factor of an expression

In greatest common factor, finding the greatest common factor of numbers was the goal. In this lesson, we will do the same thing, but we will take the concept to the next level by looking for the greatest common factor of expressions.

As you can see, 2 × 2 = 4 is the greatest factor 12 and 20 have in common, so 4 is the GCF of 12 and 20.

Find the GCF of 12x² and 20x⁴

Now, not only we need to expand 12 and 20 into their prime factorizations, we also need to do the same for x² and x⁴ as demonstrated in the figure above.

As you can see from the figure above, the GCF of 12x² and 20x⁴ is 2 × 2 × x × x = 4x²

A few more examples showing how finding the greatest common factor of expressions work

Example #1

Find the GCF of 15x⁴, 25x³, and 75x⁵

First take a look at the figure below and study it carefully.

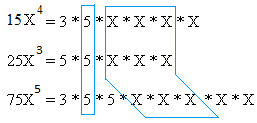
Thus, the GCF for 15x⁴, 25x³, and 75x⁵ is 5 × x × x × x = 5x³

There is a faster way to find the greatest common factor of an expression.

For example, the greatest common factor of x⁴, x³, and x⁵ is x³ since x³ is the expression with the smallest exponent. By the same token, the greatest common factor of 3², 3⁴, and 3³ is 3² since 3² is the expression with the smallest exponent.

Example #2

Find the GCF of w³ + w² + w 

We can break down this trinomial into three separate expressions: w³, w², and w.

Since w is the expression with the smallest exponent, w is the greatest common factor.

Example #3

Find the GCF of 4w⁵ + 8w⁴ + 16w³

4w⁵ + 8w⁴ + 16w³ = 2²w⁵ + 2³w⁴ + 2⁴w³

We can break down this trinomial into three separate expressions: 2²w⁵,2³w⁴,and 2⁴w³

For 2², 2³, and 2⁴, the GCF is 2²

For w⁵, w⁴, and w³, the GCF is w³

Therefore, the GCF of 4w⁵ + 8w⁴ + 16w³ is 2²w³ or 4w³

Finding the greatest common factor quiz. See how well you understand this lesson.