Introduction to the History of Fractions
Understanding fractions is fundamental to grasping various mathematical concepts. Before delving into the history of fractions, it is beneficial to familiarize yourself with the Egyptian numeration system, as it laid the groundwork for early fractional representations. This lesson explores the evolution of fractions, tracing their origins from ancient Egypt to their modern-day notation and usage.
Egyptian Numeration System and Early Fractions
The history of fractions can be traced back to around 1600 B.C. in ancient Egypt, where an extensive treatment of fractions was documented in the Rhind Papyrus. This ancient manuscript showcased the mathematical prowess of Egyptian mathematicians, highlighting their unique approach to expressing fractions.
Unlike the ratios we use today, such as 2:5 or 2/5, the Egyptians did not represent fractions as simple ratios. Instead, they employed unit fractions—fractions where the numerator is 1 and the denominator is a positive integer. This method of representation was distinct and systematic, setting the foundation for their mathematical calculations.
Understanding Unit Fractions
A unit fraction is defined as a fraction with a numerator of 1 and a positive integer as the denominator. Examples of unit fractions include 1/2, 1/5, and 1/6. The Egyptians utilized these unit fractions to express more complex fractions by breaking them down into sums of unit fractions.
For instance, the fraction 1/18 was written using specific Egyptian symbols, as illustrated in the figure below:
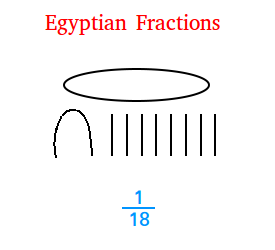 Figure 1
Figure 1Figure 1: Egyptian Representation of 1/18
In addition to numerical symbols, the Egyptians incorporated shapes into their notation. Notably, an ellipse resembling an open mouth was used to denote fractions, adding a visual element to their mathematical expressions.
Adding Fractions in Ancient Egypt
One of the intriguing aspects of Egyptian mathematics is their method of adding fractions. Unlike our current approach, the Egyptians expressed sums of fractions using only unit fractions. For example, to represent 2/5, they would decompose it into the sum of two unit fractions:
This method ensured that each component of the sum was a unit fraction, adhering to their numerical conventions. The Egyptians also had specific symbols to represent these operations. The equation 1/3 + 1/15 would be depicted using their unique symbols, as shown below:
Figure 2: Egyptian Representation of 1/3 + 1/15
A notable feature in their notation was the use of the man’s feet symbol. The direction in which the feet pointed indicated the operation to be performed:
- Pointing towards the direction of writing: Indicates addition.
- Pointing away from the direction of writing: Indicates subtraction.
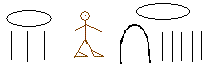
In the example above, the feet are pointing towards the writing direction, signifying that the fractions should be added.
Transition to Modern Fraction Notation
The way we represent fractions today has evolved significantly from the ancient Egyptian system. The modern fractional notation likely has its roots in the Hindu mathematical tradition. Around A.D. 630, the Indian mathematician Brahmagupta introduced a new way of writing fractions. Unlike the Egyptians, Brahmagupta wrote fractions without using a bar, representing two-fourths simply as:

This representation marked a shift towards the more familiar form of fractions used today.
Contributions of Hindu and Arabic Mathematicians
Following the Hindu tradition, the Arab mathematicians made significant contributions to the notation of fractions. They introduced the fraction bar, which allowed for clearer and more standardized representation of fractions, such as 2/4. However, the use of the fraction bar was initially limited due to typesetting constraints.
The concepts of numerator and denominator—terms that describe the components of a fraction—originated from Latin writers. These terms helped in formalizing the language around fractions, making mathematical communication more precise.
Advancements in Fraction Operations
Up until the sixteenth century, mathematical operations involving fractions were relatively rudimentary. When dealing with fractions, the common denominator was typically found by simply multiplying the denominators together. For example, to add 1/3 and 1/4, the common denominator would be 12 (since 3 × 4 = 12), and the fractions would be adjusted accordingly:
However, in the seventh century, mathematicians began to use the least common multiple (LCM) extensively when adding and subtracting fractions. This approach made calculations more efficient by reducing the size of the denominators involved.
Multiplication of Fractions
The multiplication of fractions as we understand it today has remained largely unchanged for centuries. The process involves multiplying the numerators together and the denominators together. For example:
This method has provided a consistent and straightforward way to handle multiplication involving fractions, ensuring clarity and ease of use in mathematical computations.
Division of Fractions: A Historical Perspective
Division of fractions has a more complex history, with methods differing significantly from contemporary practices. Historically, two primary methods were employed:
1. Common Denominator Method:
In this approach, mathematicians would first find a common denominator for the fractions involved, even though this step is unnecessary in modern division of fractions. For example, to divide 4/2 by 2/3, they would adjust the fractions to have a common denominator before performing the division:
2. Cross-Multiplication Method: This method involves multiplying across the numerators and denominators directly. Using the same example:
This approach is more aligned with how we perform division of fractions today, emphasizing efficiency and simplicity.
These historical methods highlight the evolution of mathematical operations and how our current techniques have been refined over time for greater effectiveness.
Conclusion: The Evolution of Fractions
The journey of fractions from ancient Egypt to the present day is a testament to the enduring importance of this mathematical concept. Starting with the Egyptian reliance on unit fractions and unique symbolic representations, fractions have undergone significant transformations influenced by Hindu and Arabic mathematicians. The introduction of the fraction bar, the formalization of numerator and denominator terms, and the refinement of arithmetic operations have all contributed to the sophisticated and versatile system of fractions we use today.
Understanding this historical progression not only enriches our appreciation for mathematics but also underscores the collaborative and cumulative nature of mathematical advancements across different cultures and eras. As we continue to build upon these foundations, the study of fractions remains a vital component of mathematical education and application.