How to Solve Literal Equations

Recommended for You

Not sure where to start? These are the lessons and games we recommend most to students, parents and teachers on Basic-mathematics.com. Each lesson explains the topic in plain language, walks you through worked examples step by step, and ends with practice so you can check your understanding. Pick one below, or use the menu to find lessons on fractions, algebra, geometry, statistics and more.

Here, you will learn how to solve literal equations with some carefully chosen examples.

What is a literal equation?

It is an equation that has many variables and we need to solve for one of the variables.

The first literal equation we will solve is ax = b. Study this first one below carefully!

Then we will show how to solve y  = mx + b which is also a literal equation.

See below a more detailed guideline showing how to solve y = mx + b for x as we solve 8 = 2x + 4 for x. 

How to solve literal equations

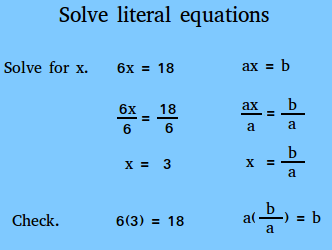
 y = mx + b

 Subtract b from both sides

 y - b = mx + b - b

 y - b = mx

 Divide both sides by m

 (y - b) / m   =   (m/m)x

 ( y - b) / m  = 1x

 (y - b) / m  = x

 8 = 2x + 4

 Subtract 4 from both sides

 8 - 4 = 2x + 4 - 4

 8 - 4 = 2x    

 Divide both sides by 2

 (8 - 4) / 2 = (2 / 2) x

 (8 - 4) / 2 = 1x

 (8 - 4) / 2 = x


We can see that the process is similar whether we are solving a literal equation or not.
All we need to do is to isolate things. For (8 - 4) / 2 = x though, we can take a step further by doing the math since we are dealing with numbers.

Therefore, x = (8 - 4) / 2 = 4 / 2 = 2

Hopefully, this example was clear enough to put you on the right track.  

More examples showing how to solve literal equations.

1)

Solve 2a + b = d for b

2a + b = d

We need to isolate b, therefore, get rid of  2a by subtracting 2a from both sides of the equation.

2a - 2a + b = d - 2a

0 + b  = d - 2a

      b   = d - 2a

2)

Solve V = lwh for w.

We need to get rid of lh. Rewrite the equation.

   V =  lhw

Get rid of lh by dividing both sides of the equation by lh

  V / lh   = (lh / lh)w

  V / lh  = 1w

  V / lh = w

3)

Solve x =
a + b + c / 3
  for c


Multiply both sides of the equation by 3

3 × x =
a + b + c / 3
×3


3x = a + b + c

We need to get rid of a and b.

Subtract a from both sides

3x  - a  = a - a + b + c

3x - a  = 0 + b + c

3x - a = b + c

Subtract b from both sides

3x - a - b = b - b + c

3x - a  - b = 0 + c

3x - a - b  =  c

4)

Solve 2(x + y) = z for y

First isolate x + y by getting rid of 2. To get rid of 2, divide both sides by 2.

2 / 2 (x  + y)   = z / 2

1(x + y)   = z / 2

x + y = z / 2

Subtract x from both sides of the equations

x - x + y  = (z / 2) - x

0  + y   = (z / 2) - x

y = (z / 2) - x