Inequality with all real numbers as solutions
An inequality with all real numbers as solutions is easy to solve or easy to recognize. See a few examples below.
Example #1
Solve x - x > -1
x - x > -1
x - x = 0, so we get 0 > -1
Since 0 is always bigger than -1, this inequality is always true. Therefore, all real numbers are solutions.
Example #2
Solve 5x + x + 3 > 6x + -4
5x + x + 3 > 6x + -4
Subtract 3 from each side of the inequality
5x + x + 3 - 3 > 6x + -4 - 3
5x + x + 0 > 6x + -4 + -3
5x + x > 6x + -7
Simplify by adding 5x and x
6x > 6x + -7
Subtract 6x from each side of the inequality
6x - 6x > 6x - 6x + -7
0 > 0 + -7
0 > -7
Since 0 is always bigger than -7, this inequality is always true. Therefore, all real numbers are solutions.
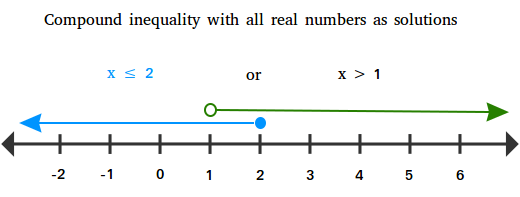
Compound inequality with all real numbers as solutions
Example #3
Solve 8x + 4 ≤ 20 or 3x - 2 > 1
Solve 8x + 4 ≤ 20
8x + 4 ≤ 20
Subtract 4 from each side of the inequality
8x + 4 - 4 ≤ 20 - 4
8x ≤ 16
Divide each side by 8
8x/8 ≤ 16/8
x ≤ 2
Solve 3x - 2 > 1
3x - 2 > 1
Add 2 to each side of the inequality
3x - 2 + 2 > 1 + 2
3x - 2 + 2 > 1 + 2
3x > 3
Divide each side by 3
3x/3 > 3/3
x > 1
The solution is x ≤ 2 or x > 1 and this includes all real numbers as shown in the graph below.
Absolute value inequality with all real numbers as solutions
Example #4
Solve |x| > -10
The absolute value of a number is always positive.
For example, suppose x is positive and choose x = 2
|2| = 2 and 2 is always bigger -10
Suppose x is negative and choose x = -2
|-2| = 2 and 2 is always bigger than -10
Therefore, |x| > -10 has all real numbers as solutions
No matter what number you choose for x, when you take the absolute value, it will always be bigger than -10.
In general, if |x| > a and a is a negative number, |x| > a has all real numbers as solutions.
Recent Articles
-
How To Find The Factors Of 20: A Simple Way
Sep 17, 23 09:46 AM
There are many ways to find the factors of 20. A simple way is to... -
The SAT Math Test: How To Be Prepared To Face It And Survive
Jun 09, 23 12:04 PM
The SAT Math section is known for being difficult. But it doesn’t have to be. Learn how to be prepared and complete the section with confidence here.
100 Tough Algebra Word Problems.
If you can solve these problems with no help, you must be a genius!
