|
 |
|||||
Intersection of setsThis lesson will explain how to find the intersection of sets. We will start with a definition of the intersection of two sets Given two sets A and B, the intersection is the set that contains elements or objects that belong to A and to B at the same time We write A Ç B Basically, we find A Ç B by looking for all the elements A and B have in common. We next illustrate with examples Example #1. To make it easy, notice that what they have in common is in bold Let A = {1 orange, 1 pinapple, 1 banana, 1 apple} and B = { 1 spoon, 1 orange, 1 knife, 1 fork, 1 apple} A Ç B = {1 orange, 1 apple} Example #2. 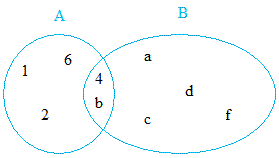Find the intersection of A and B and then make a Venn diagrams. A = {b, 1, 2, 4, 6} and B = { 4, a, b, c, d, f} A Ç B = {4, b}  Example #3. A = { x / x is a number bigger than 4 and smaller than 8} B = { x / x is a positive number smaller than 7} A = { 5, 6, 7} and B = { 1, 2, 3, 4, 5, 6} A Ç B = {5, 6} Or A Ç B = { x / x is a number bigger than 4 and smaller than 7} Example #4. A = { x / x is a country in Asia} B = { x / x is a country in Africa} Since no countries in Asia and Africa are the same, the intersection is empty A Ç B = { } Example #5.  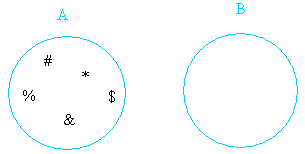A = {#, %, &, *, $ } B = { } This example is subtle! Since the empty set is included in any set, it is also included in A although you don't see it Therefore, the empty set is the only thing set A and set B have in common A Ç B = { } In fact, since the empty set is included in any set, the intersection of the empty set with any set is the empty set. Definition of the union of three sets: Given three sets A, B, and C the intersection is the set that contains elements or objects that belong to A, B, and to C at the same time We write A Ç B Ç C Basically, we find A Ç B Ç C by looking for all the elements A, B, and C have in common. 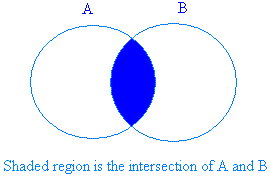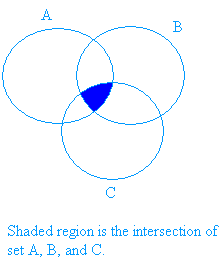A = {#, 1, 2, 4, 6}, B = {#, a, b, 4, c,} and C = A = {#, %, &, *, $, 4 } A Ç B Ç C = {4 , # } The graph below shows the shaded region for the intersection of two sets  The graph below shows the shaded region for the intersection of three sets  This ends the lesson about intersection of sets. If you have any questions about the intersection of sets, I will be more than happy to answer them.
 |
|
|||||
IntroductionArithmeticGeometryGraph it!Probability and statisticsReal life mathSequences and patternsAlgebraResourcesTeachers!
|
||||||
| Powered by Site Build It | ||||||
|
| ||||||
