Interval notation
We use interval notation to represent subsets of real numbers. Suppose that a and b are real numbers such that a < b.
Then, the open interval (a,b) represents the set of all real numbers between a and b, except a and b.
- { x / a < x < b} is the set-builder notation.
- a < x < b is the inequality description.
- (a, b) is the interval notation.
The closed interval [a,b] represents the set of all real numbers between a and b, including a and b.
- { x / a ≤ x ≤ b} is the set-builder notation.
- a ≤ x ≤ b is the inequality description.
- [a, b] is the interval notation.
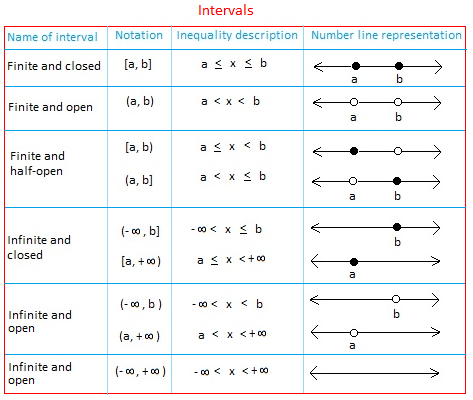
The table below lists nine types of intervals used to describe subsets of real numbers. Notice the number line representation of each interval.
Basically, an interval is a set containing all numbers between two given numbers or endpoints. The set may have one, both, or neither of the two given numbers.
An interval is open if the interval does not contain its endpoints.
The symbols ( or ) called parentheses or round brackets are used to indicate that an endpoint is not included in the interval.
An interval is closed if the interval contains its endpoints.
The symbols [ or ] called brackets are used to indicate that an endpoint is included in the interval.
Sometimes, the interval may contain only one of its endpoints. In this case, the interval is half-open. The interval [2, 8) is half-open. It contains 2 and all numbers between 2 and 8. Notice that 8 is not included since the interval is open at 8.
-∞ means minus infinity and +∞ means positive infinity.
Both -∞ and +∞ are used to show that an interval is unbounded or extends indefinitely to the left or to the right respectively.
Why do we need intervals? They can be used to describe the domains of functions, bounds for estimates, and the solution sets of equations and inequalities.
The length of an interval with endpoints a and b with a < b is b - a.
Converting an inequality to interval notation
Express each inequality in interval notation.
Examples
Inequality Interval notation
-6 ≤ x < 1 [-6, 1)
x > 20 (20, ∞)
x ≥ -1 or x < -4 (-∞, -4) U [-1,∞)
Check this site if you want to learn more about inequalities and interval notation.