Mutually exclusive events

Mutually exclusive events are events that cannot occur together. In other words these events do not have any common outcomes.

Consider the following 2 events when throwing a die once.

Let B = an even number is observed

Let A = an odd number is observed

B  = { 2, 4, 6 }               A = { 1, 3, 5 }

Do the events  {1, 3, 5} and { 2, 4, 6 } have anything in common?

No they don't. Therefore, {2, 4, 6 } and {1, 3, 5 } are mutually exclusive events.

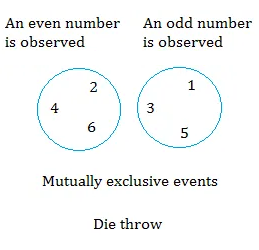
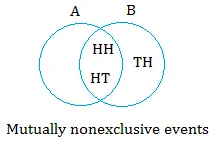
Suppose you flip a coin twice.

Let A = the first toss results in head

Let B = the tosses results at most 1 tail

A  = { HH, HT }

B ={ HH, HT, TH }

Do the events { HH, HT }  and { HH, HT, TH } have anything in common?

Yes, these events have HH and HT in common. Therefore, A and B are not mutually exclusive events.

A couple more example of events that are mutually exclusive and events that are mutually nonexclusive.

1)  

A superintendent selects a student randomly from a school district to see if the student passed a state test.

Let A  = the student passed the test

Let B = the student did not pass the test

Since a student cannot pass and fail the test at the same time, these two events are mutually exclusive events.

2)

A card is picked randomly from a deck of 52 cards.

Let A =  the card is a 5

Let B = the card is a diamond.

Since 5 of diamonds will belong to both events, A and B mutually nonexclusive events.