Pressure in a liquid
The pressure in a liquid also called hydrostatic pressure is the force that a liquid can exert on things. The formula to use to calculate the pressure due to a liquid is the following:
Liquid pressure = weight density × depth
or
Liquid pressure = ρ × g × depth
Next, we show you how we got this formula using some basic math. Consider the container you see above that contains a liquid.
It is the weight of the liquid above that exerts some pressure on the base or bottom of the container, so the formula becomes.
We saw in the lesson about density that
Similarly,
weight = weight density × volume
volume = area × height
weight = weight density × area × height
Replace the weight with weight density × area × height in the formula for pressure above.
Whenever you see the same thing on top and at the bottom, it gets cancelled. As a result, the area shown in bold below will cancel.
It is common to use the word depth instead of height when talking about pressure in a liquid.
Pressure or liquid pressure = weight density × height
Pressure or liquid pressure = weight density × depth
Expanding the liquid pressure formula
Weight density = weight / volume
According to Newton's second law, weight = mass × g
g is the acceleration due to gravity.
Weight density = (mass × g) / volume
Weight density = (mass / volume) × g
By definition, density = ρ = mass / volume
Therefore, weight density = ρ × g
As already stated, pressure or liquid pressure = weight density × depth
After replacing weight density with ρ × g, we get:
Pressure or liquid pressure = ρ × g × depth
Why does the pressure in a liquid depend on the density?
The denser a liquid is, the heavier the liquid is and as a result, the more pressure it will exert.
For example, mercury is more dense than water and it is heavier. It will as a result exert more pressure. Don't believe me? Just measure the weight of the same amount of mercury and water.
Why does the pressure in a liquid depend on the depth?
Suppose you go diving. The deeper you are, the more water are on top of you. Since there are more water pressing on your body, the pressure will be more.
The pressure in a liquid does not depend on the amount of liquid
To show this, we will use formula for pressure.
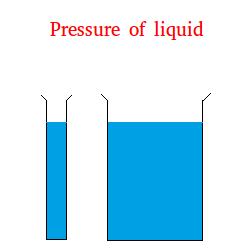
The tube on the right is 4 times as large as the tube on the left.
Let w = weight of the liquid inside the tube on the left and W = weight of the liquid inside the tube on the right.
W = 4 × w
Let a = area where the pressure is applied to the bottom of the tube on the left
Let A = area where the pressure is applied to the bottom of the tube on the right.
A = 4 × a
Since 4 is on top and at the bottom, it will cancel. As you see, the pressure is still the same.
This makes sense since if you are swimming at the same height in a big lake or in a swimming pool, the pressure is still the same.
Do you see also why shape does not matter? Check this page about Pascal's vases. You
will notice that the water is at the same level in each vase regardless
of the shape. It is so because the pressure is equal at the bottom of
each vase. If the pressures were not equal, water will flow.