Probability of compound events
The probability of compound events combines at least two simple events, either the union of two simple events or the intersection of two simple events. The probability that a coin will show head when you toss only one coin is a simple event.
However, if you toss two coins, the probability of getting 2 heads is a compound event because once again it combines two simple events.
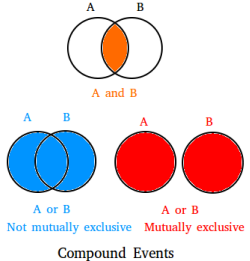
Added to the fact that you could be looking for the intersection or the union, the events could either be independent events or dependent events. Moreover, the union could be mutually exclusive or mutually inclusive. There are many different possibilities and different compound probability formulas as a result. You could end up investigating any of the following compound probability to see if it is possible.
- The intersection of two independent events
- The intersection of two dependent events
- The union of two dependent and mutually inclusive events
- The union of two independent and mutually inclusive events
- The union of two dependent and mutually exclusive events
- The union of two independent and mutually exclusive events
How to find the probability of the intersection of two independent events?
Example #1
Suppose you say to a friend, " I will give you 10 dollars if two coins land on head."
Let's see what happens when your friend toss two coins:
If heads = H and tails = T, the different outcomes are HH, HT, TH, or TT.
As you can see, out of 4 possibilities, only 1 will give you HH.
Your friend has 25% chance of getting 10 dollars since one-fourth = 25%.
The example above is a good example of independent events. What are independent events?
When you toss the two coins, neither coin has the power to influence the other coin. When the outcome of one event does not affect the outcome of another event, the two events are said to be independent. This compound event is independent then.
When two events are independent, you can use the following formula:
probability(A and B) = probability(A) × probability(B)
probability(H and H) = P(H) × P(H) and P(H) = 1/2
| probability(H and H) = |
1
2
|
× |
1
2
|
| probability(H and H) = |
1
2
|
× |
1
2
|
How to find the probability of the intersection of two dependent events?
Sometimes, compound events can be dependent. What are dependents events? When the outcome of one event has the power to affect the outcome of another event, the two events are said to be dependent.
When two events are dependent, you can use the following formula:
probability(A and B) = probability(A) × probability(B / A)
Example #2
Suppose, a bag has 4 red balls and 6 blue balls. What is the probability of choosing 2 blue balls at random without replacement?
These events are dependent since after you choose one blue ball, it changes the number of blue balls and the number of balls all together.
Blue ball #1:
Blue ball #2:
Now there are 5 blue balls and 9 balls all together.
Let Blue = B
probability(B and B) = probability(B) × probability(B / B)
probability(B / B) is the probability that the second ball is blue if the first ball drawn was blue.
| probability(B and B) = |
6
10
|
× |
5
9
|
| probability(B and B) = |
6
10
|
× |
5
9
|
You have 33.33% chance of doing this since 1/3 is equal to 33.33%
Lastly, sometimes, as opposed to having two events happening at the same time, you may need to choose between two events.
When two events cannot both occur, they are called mutually exclusive events.
How to find the probability of the union of two dependent and mutually inclusive events
When two events are mutually inclusive, it means the two events can happen at the same time. If two events are mutually inclusive, they will in many cases depend on each other.
You can use the following formula:
probability(A U B) = probability(A) + probability(B) - P(A ∩ B)
probability(A U B) = probability(A) + probability(B) - P(A) × P(B / A)
Example #3
What is the probability of selecting a black card or a 3 when a card is randomly selected from a deck of 52 cards?
 standard deck of cards
standard deck of cards26 cards are black and 26 cards are red
The number of cards labeled with the number 3 is 4
The number of black cards labeled with the number 3 is 2
A is the event 'a black card is drawn' and P(A) = 26/52
B is the event 'a 3 is drawn' and P(B) = 4/52
A ∩ B is the event 'a black card with the number 3 on it is drawn' and P(A ∩ B) = 2/52
probability(A U B) = probability(A) + probability(B) - P(A ∩ B)
probability(A U B) = 26/52 + 4/52 - 2/52
probability(A U B) = (26 + 4 - 2)/52 = 28/52 = 0.538
Notice that P(black ∩ 6) = P(black) × P(6 / black) = 26/52 × 2/26 = 2/52
Similarly, P(black ∩ 6) = P(6) × P(black / 6) = 4/52 × 2/4 = 2/52
How to find the probability of the union of two independent and mutually inclusive events
When two events are mutually inclusive, it means the two events can happen at the same time. If two events are also independent, P(A ∩ B) = P(A) × P(B) and you can use the following formula shown in bold:
probability(A U B) = probability(A) + probability(B) - P(A ∩ B)
probability(A U B) = probability(A) + probability(B) - P(A) × P(B)
Example #4
Suppose that the probability that you will graduate from university is 0.80 and the probability that your sister will graduate from university is 0.90. What is the probability that you or your sister will graduate from university.
Let A be the event that you will graduate from university. P(A) = 0.80
Let B be the event that your sister will graduate from university. P(B) = 0.90
A and B are mutually inclusive events since it is possible that both you and your sister could graduate from university.
A and B are independent events. No matter what your sister tries to do to prevent you from graduating, you can argue that your future in is your hand to a great extent and vice versa.
probability(A U B) = probability(A) + probability(B) - P(A) × P(B)
probability(A U B) = 0.80 + 0.90 - 0.80 × 0.90
probability(A U B) = 1.7 - 0.80 × 0.90
probability(A U B) = 1.7 - 0.72
probability(A U B) = 0.98
The likelihood that you or your sister will graduate from university is 98%.
How to find the probability of compound events when the events are mutually exclusive and dependent
Mutually exclusive events are events that cannot happen at the same time. Suppose A and B are two events. Since A and B cannot occur at the same time, P(A ∩ B) = 0
To find the probability of compound events when the events are mutually exclusive, use the formula for non-mutually exclusive events and set P(A ∩ B) equal to zero.
Suppose A and B are mutually exclusive events, then you can use the formula shown in bold.
probability(A U B) = probability(A) + probability(B) - P(A ∩ B)
probability (A or B) = probability (A) + probability (B)
Example #5
Suppose you and your brother both throw a die. Whoever get a 4 wins!
These are mutually exclusive events because you cannot both win this game.
These are dependent events also because your win depends on how bad your brother plays and vise versa.
Let Y = you win and B = your brother win
probability (Y or B) = probability (Y) + probability (B)
You:
Your brother:
probability(Y or B) = probability(Y) + probability(B)
| probability(Y or B) = |
1
6
|
+ |
1
6
|
| probability(Y or B) = |
1
6
|
+ |
1
6
|
Is it possible to find the probability of the union of two independent and mutually exclusive events?
If two events are independent, P(A ∩ B) = P(A) × P(B)
If two events are mutually exclusive, P(A ∩ B) = 0
As a result, P(A) × P(B) = 0
We get either P(A) = 0, P(B) = 0, or both P(A) and P(B) = 0
As you can see, it is not possible for two events to be independent and mutually exclusive without using a probability that is equal to zero either for one of the events or both. A probability of zero means that the event will never happen.