Proof of the law of sines
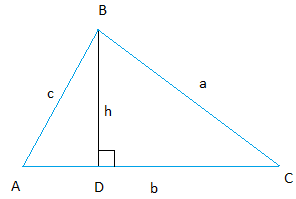
An easy to follow proof of the law of sines is provided on this page. Start with a scalene triangle ABC.
Proof of the law of sines: part 1
Draw an altitude of length h from vertex B. Call it D, the point where the altitude meets with line AC.
Two triangles ABD and CBD are formed and they are both right triangles.
We can then use the definition of the sine of an angle of a right triangle.
|
Using triangle ABD, sin A =
h
c
|
Using triangle CBD, sin C =
h
a
|
After solving each equation for h, we get:
|
h = sin A × c |
h = sin C × a |
h = sin A × c = sin C × a
sin A × c = sin C × a (1)
Divide both sides of equation (1) by sin A sin C. Then, notice that anything in bold gets cancelled.
|
sin A × c
sin A sin C
|
=
sin C × a
sin A sin C
|
|
sin A × c
sin A sin C
|
=
sin C × a
sin A sin C
|
Part 1 of the proof is shown below
|
c
sin C
|
=
a
sin A
|
Part 1 of the proof is shown below
|
c
sin C
|
=
a
sin A
|
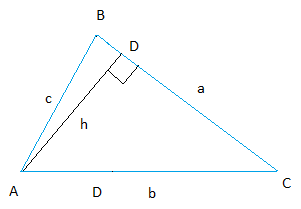
Proof of the law of sines: part 2
Start with the same triangle ABC. This time though, draw the altitude from A. Two triangles ABD and ACD are formed and they are both right triangles.
|
Using triangle ABD, sin B =
h
c
|
Using triangle ACD, sin C =
h
b
|
|
h = sin B × c |
h = sin C × b |
h = sin B × c = sin C × b
sin B × c = sin C × b (2)
Divide both sides of equation (2) by sin B sin C. Then, notice that anything in bold gets cancelled.
|
sin B × c
sin B sin C
|
=
sin C × b
sin B sin C
|
|
sin B × c
sin B sin C
|
=
sin C × b
sin B sin C
|
Part 2 of the proof is shown below
|
c
sin C
|
=
b
sin B
|
Part 2 of the proof is shown below
|
c
sin C
|
=
b
sin B
|
Combining part 1 and part 2, we get the following law of sines.
|
a
sin A
|
=
b
sin B
|
=
c
sin C
|
|
a
sin A
|
=
b
sin B
|
=
c
sin C
|