Properties of zero
The two properties of zero are the addition property of zero and the multiplication property of zero.
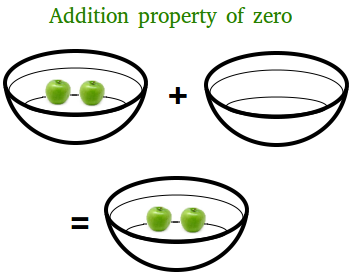
The figure below illustrates the addition property of zero and it can be written as 2 + 0 = 2
Addition property of zero:The addition property of zero says that a number does not change when adding or subtracting zero from that number.
Examples showing the addition property of zero
4 + 0 = 4
12 + 0 = 12
5 − 0 = 5
48 − 0 = 48
0 + 1 = 1
a − 0 = a
x + 0 = x
0 − 12 = -12
(a + b) + 0 = a + b
0 − y = -y
Formal definition of the addition property of zero
For every number real number a, a + 0 = a and 0 + a = a
Multiplication property of zero
The multiplication property of zero says that zero times any number is equal to zero.
Examples
2 × 0 = 0
0 × 12 = 0
-5 × 0 = 0
23344555677888882 × 0 = 0
x × 0 = 0
(x + y + z + r )× 0 = 0
Formal definition of the multiplication property of zero
For every number real number a, a × 0 = a and 0 × a = 0
The different names given to the addition property of zero or the multiplication property of zero
The different names given to the addition property of zero
- Addition property of zero
- Identity property of zero
- Additive property of zero
- Zero property of addition
- Identity property of addition
- Additive identity property
The different names given to the multiplication property of zero
- Multiplication property of zero
- Multiplicative property of zero
- Zero property of multiplication
Other properties of zero
Division by zero is undefined or has no answer. For example, 9/0 has no answer.
The number 0 is called the additive identity.
Any number to the power of 0 is equal to 1.
0 is neither positive nor negative.
0 is neither prime nor composite.
Additive inverse propertyIf you add two numbers and the sum is zero, we call the two numbers additive inverses or opposites of each other.
For example, 2 is the additive inverse of -2 because 2 + -2 = 0
-2 is also the additive inverse of 2 because -2 + 2 = 0