Proportions

This lesson about proportions will teach you some very important concepts you need to know. You should review the lesson about ratio before studying this lesson. Also, take the quiz below to see how much you know!

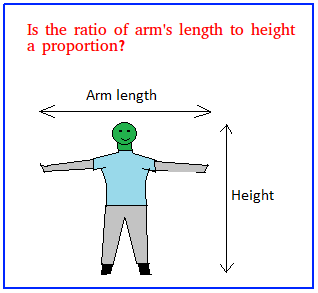
Take a look at the image below. Try to measure the ratio of arm's length to height for 5 people that you know. What did you notice? More on this later, so keep reading!

Look at the following two ratios. Right now they are just ratios.

Do they form a proportion? They will form a proportion if the ratios are equal, so first put an equal sign between them. Then, you have two choices to check if the ratios are equal.

Choice #1: You can just convert both ratios into decimals and see if the decimals are equal.

3 / 5 = 0.60   6 / 12 = 0.5

Since 0.60 ≠ 0.50, the ratios are not equal and therefore do not for a proportion.

Choice #2:

You can also tell if two ratios are equal by comparing their cross products. If the cross products are equal, then they form a proportion.

Recall that a cross product is obtained when you multiply the numerator of one fraction by the denominator of another fraction.

3 × 12 = 36 and 5 × 6 = 30. 

Since 36 is not equal to 30, 3/5 and 6/12 do not form a proportion.

Do the following ratios form a proportion?

10 × 8 = 80 and 16 × 5 = 80

80 is equal to 80, therefore, they form a proportion.

Suppose the following is a proportion

Then, the proportion can also be written as a:b::c:d

We can read a:b::c:d  as " a is to b as c is to d "

The format above make it easy also to identify the means and the extremes.

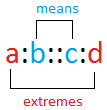
In any proportion the product of the extremes is equal to the product of the means. It is just a different way of wording the procedure of cross multiplication.

Fourth proportional:

Looking at a:b::c:d, the fourth term is d. We call d fourth proportional.

Equivalent proportions:

You can get an equivalent proportion by inverting each ratio:

a:b::c:d is the same as b:a::d:c

You can get others equivalent proportions by interchanging either the means, the extremes or both

a:b::c:d is the same as a:c::b:d, d:b::c:a and d:c::b:a

Thinking a little deeper about proportions

Wages:

Is your wage or the money you make per hour a proportion? As long as the wage stays the same, it will form a proportion.

Suppose you make 25 dollars per hour and work 8 hours a day.

Money per hour is 25:1

Money at the end of the day is 200:8

Let us see if 25:1::200:8 form a proportion

Product of means is 1 × 200 = 200

Product of extremes is 25 × 8 = 200

Ratio of arm's length to height:

Let us now talk about the picture shown at the beginning of this lesson.

In adult males, arm's length is about 5 cm greater than the height.

Is it ok to say that the ratio of arm's length to height form a proportion for adult males?

If you are willing to neglect the tiny differences and use exactly 5 cm, the answer is yes.

Say your husband's height is 152.4 centimeter, the arm length is then 152.4 + 5 = 157.4

Now, if you are a male and your height is 165 centimeter, the arm length is then 165 + 5 = 170

157.4 / 152.4 = 1.03032 

170 / 165 = 1.03030

Since the ratios are closely equal, you could make a claim and say that ratio of arm's length to height for adult males form a proportion.