Prove that the diagonals of an isosceles trapezoid are congruent

In order to prove that the diagonals of an isosceles trapezoid are congruent, consider the isosceles trapezoid shown below. In this lesson, we will show you two different ways you can do the same proof using the same trapezoid.

The first way is to show that triangle ABC is congruent to triangle DCB

Given: Isosceles trapezoid ABCD with segment AB ≅ segment DC

Prove: segment AC ≅ segment BD

Since the trapezoid is isosceles, the base angles are congruent.

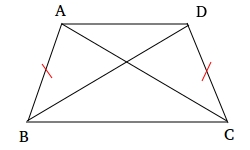
Therefore, ∠CBA ≅ ∠BCD

Furthermore, segment BC ≅ to segment BC by the reflexive property of congruence.

By SAS Postulate, triangle ABC ≅ triangle DCB.

Therefore, segment AC ≅ segment BD

Things that you need to keep in mind when you prove that the diagonals of an isosceles trapezoid are congruent.

Here are some things that you must know about the proof above. 

• The statement if a trapezoid is isosceles, then the base angles are congruent requires also a proof. However, we will not prove here. 

• The sides that are equal in an isosceles trapezoid are always the sides that are not parallel. In the trapezoid above, we show these sides with the red marks.

• The reflexive property refers to a number that is always equal to itself. For example, 9 = 9 or y = y are examples of the reflexive property. 

• SAS stands for "side, angle, side". You should perhaps review the lesson about congruent triangles.

• In order to prove that the diagonals of an isosceles trapezoid are congruent, you could have also used triangle ABD and triangle DCA. 

Another great way to prove that the diagonals of an isosceles trapezoid are congruent. This time we show that triangle BAD is congruent to triangle CDA

Given: Isosceles trapezoid ABCD with segment AB ≅ segment DC

Prove: segment AC ≅ segment BD

Since the trapezoid is isosceles, the base angles are congruent

Therefore, ∠BAD ≅ ∠CDA

Furthermore, segment AD ≅ to segment AD by the reflexive property of congruence.

By SAS Postulate, triangle BAD ≅ triangle CDA

Therefore, segment AC ≅ segment BD