Pythagorean Theorem
Explore the Pythagorean theorem with the interactive lesson below. See how the area of the red square + the area of the blue square is equal to the area of the gray square.
Tips: to find the area of a square, just count the number of small squares inside of it. Align to Grid or Rotate the gray square so you can easily count the number of small squares inside of the squares.
Interactive Pythagorean Theorem
Quiz
What is the Pythagorean theorem?
The Pythagorean Theorem was named after famous Greek mathematician Pythagoras. It is an important formula that states the following: a2 + b2 = c2
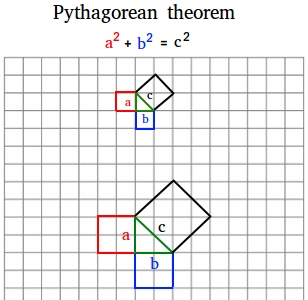
Looking at the figure above, did you make the following important observation? This may help us to see why the formula works.
- The red square has 2 triangles in it
- The blue square has also 2 triangles in it
- The black square has 4 of the same triangle in it
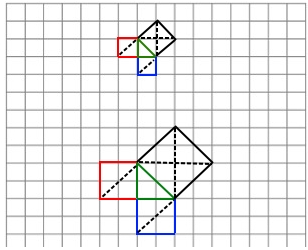
Therefore, area of red square + area of blue square = area of black square
Let a = the length of a side of the red square
Let b = the length of a side of the blue square
Let c = the length of a side of the black square
Therefore, a2 + b2 = c2
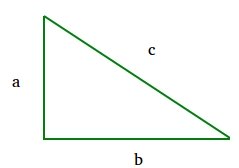
Thus, given two sides, the third side can be found using the formula.
We will illustrate with examples, but before proceeding, you should know how to find the square root of a number and how to solve one-step equations.
Examples showing how to use the Pythagorean theorem
Exercise #1
Let a = 3 and b = 4. Find c, or the longest side
c2 = a2 + b2
c2 = 32 + 42
c2= 9 + 16
c2 = 25
c = √25
The sign (√) means square root
c = 5
Exercise #2
Let c = 10 and a = 8. Find b, or the other leg.
c2 = a2 + b2
102 = 82 + b2
100 = 64 + b2
100 - 64 = 64 - 64 + b2 (minus 64 from both sides to isolate b2 )
36 = 0 + b2
36 = b2
b = √36 = 6
Exercise #3
Let c = 13 and b = 5. Find a
c2 = a 2+ b2
132 = a2 + 52
169 = a2 + 25
169 - 25 = a2 + 25-25
144 = a2 + 0
144 = a2
a = √144 = 12