Quadratic functions
Quadratic functions are functions that can be written in the standard form f(x) =
ax2 + bx + c, where a ≠ 0 and a, b, and c are all constants.
The standard form has 3 different types of terms:
- ax2 is called the quadratic term
- bx is called the linear term
- c is called the constant term.
Notice that the condition that a ≠ 0 ensure that every function has a quadratic term, but not necessarily a linear term or a constant term. If a = 0, the function has no quadratic term. In that case, the function is not a quadratic function.
Graph of quadratic functions
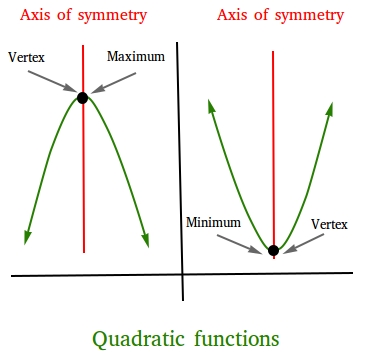
Here is how the graph of quadratic functions will look like. Notice the axis of symmetry and the vertex that can either be a maximum or a minimum.
Examples of quadratic functions
f(x) = 2x2 + 3x + -4
f(x) = 2x2 - 3x + 5
f(x) = -x2 + x + 100
f(x) = 3x2 + 6x
f(x) = 5x2 + -4
f(x) = 6x2
f(x) = (x + 2)(x+3)
f(x) = 2(x - 3)2 + 4
Notice that f(x) = (x + 2)(x+3) = x2 + 3x + 2x + 6 = x2 + 5x + 6
Notice also that f(x) = 2(x - 3)2 + 4 = 2(x2 - 6x + 9) + 4 = 2x2 - 12x + 18 + 4 =
2x2 - 12x + 22
A function may appear to be a quadratic function when in fact it is not quadratic.
For example, f(x) = 4(x2 + x) - 4(x2 + 8) is not a quadratic function.
f(x) = 4(x2 + x) - 4(x2 + 8)
f(x) = 4x2 + 4x - 4x2 + -32
f(x) = 4x + -32
As you can see, this function is linear.
The three forms of quadratic functions
General form
f(x) = ax2 + bx + c, where a, b, and c are real numbers, is called the general form of a quadratic function.
Factored form
f(x) = (ax + b)(cx + d), where a, b, c, and d are real numbers, is called the factored form of a quadratic function.
Vertex form
f(x) = a(x - h)2 + k, where a, h, and k are real numbers, is called the vertex form of a quadratic function.