Relationship between degrees and radians
To obtain a relationship between degrees and radians, we can compare the number of degrees in one complete rotation and the number of radians in one complete rotation.
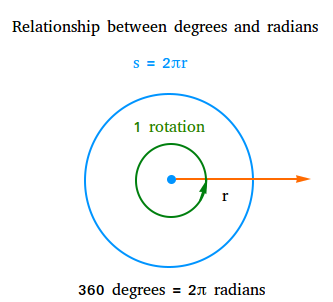
The number of degrees in one complete rotation is equal to 360 degrees.
In degrees, θ = 360 degrees
The radian measure of this central angle or θ can be found by using the formula for radian measure or θ = s / r with s = length of the intercepted arc.
In a complete rotation, the length of the intercepted arc is equal to the circumference of the circle or 2πr.
θ = s / r = circumference of the circle / r = 2πr / r = 2π
θ = 2π radians
Because in one complete rotation θ measures 360 degrees or 2π radians, 360 degrees = 2π radians
After Dividing both sides by 2, we get 180 degrees = π radians
Dividing the equation 180 degrees = π radians by 180 degrees or π gives the following conversion rules.
To convert radians to degrees, multiply radians by
180 degrees / π radians
To convert degrees to radians, multiply degrees by
π radians / 180 degrees
100 Tough Algebra Word Problems.
If you can solve these problems with no help, you must be a genius!
Recommended