Side-Splitter Theorem
The side-splitter theorem states that if a line is parallel to one side of a triangle and cross the other two sides, then the line divides those sides proportionally. Take a look at the figure below.
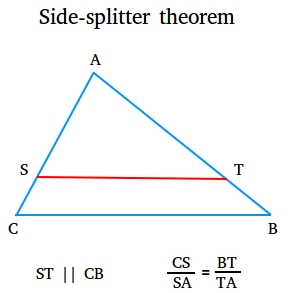
Since ST is parallel to CB, Then CS / SA = BT / TA
Note that ST is not a midline of the triangle. In other words, S is not the midpoint of CA and T is not the midpoint of BA.
Using the side-splitter theorem to solve a geometric problem.
In the figure below, AB is parallel to UT. Find x if UA = 36, TB = 9, and BS = 3.

Since AB is parallel to UT, we can use the side-splitter theorem.
UA / AS = TB / BS
Substitute
36 / x = 9 / 3
Solve for x using cross-multiplication
36 × 3 = x × 9
108 = 9x
Divide both sides by 9
108 / 9 = 9x / 9
12 = x