Solve a polynomial equation by graphing

You can solve a polynomial equation by graphing each side of the equation separately on the same coordinate system. Then, to find the solution, just get the x-values at the point of intersection.

Example

Solve x³ + 3x² = x + 3 by graphing

Step 1

Use a graphing calculator to graph y₁ = x³ + 3x² and y₂ = x + 3 on the same screen. A portion of the graph is shown below. y₁ is the graph shown in red and y₂ is the graph shown in green.

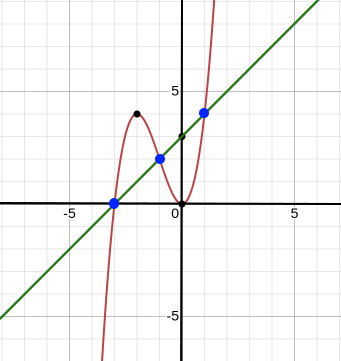
Step 2

You can use either the graph above to locate the points of intersection or you can use the intersect feature in your calculator to find the x-values at the points of intersection.

The points of intersection are shown on the graph above with blue dots. The x-values give the solution. Therefore, the solutions are -3, -1, and 1.

Check

Show that -3, -1, and 1 are indeed solutions by plugging each value in the original solution.

x = -3

x³ + 3x² = x + 3

(-3)³ + 3(-3)² = -3 + 3

-27 + 3(9) = 0

-27 + 27 = 0

0 = 0

x = -1

(-1)³ + 3(-1)² = -1 + 3

(-1)³ + 3(-1)² = -1 + 3

-1 + 3(1) = 2

-1 + 3 = 2

2 = 2

x = 1

x³ + 3x² = x + 3

(1)³ + 3(1)² = 1 + 3

1 + 3(1) = 4

1 + 3 = 4

4 = 4