How to solve tough absolute value equations

Learn how to solve tough absolute value equations with two carefully chosen examples.

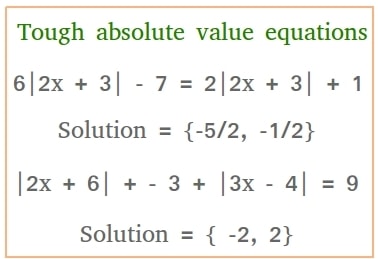
Example #1:     6|2x + 3| - 7 = 2|2x + 3| + 1

Try to have the numbers on the right side. Add 7 to both sides of the equation.

 6|2x + 3| - 7 + 7 = 2|2x + 3| + 1 + 7

 6|2x + 3|  = 2|2x + 3| + 8

Now, try to have the expressions 6|2x + 3| and 2|2x + 3| on the left side. Subtract 2|2x+3| from both sides of the equations.

6|2x + 3| - 2|2x + 3| = 2|2x + 3| - 2|2x + 3| + 8

6|2x + 3| - 2|2x + 3| =  8

Finally, you need to make an important observation.

Notice that 6|2x + 3| and -2|2x + 3| are like terms. Therefore, you can use the distributive property to simplify.

6|2x + 3| - 2|2x + 3| = (6 - 2)|2x + 3| = 4|2x + 3|


We end up with 4|2x + 3| = 8

Divide both sides of the equation by 4

(4/4)|2x + 3| = 8/4

  1|2x + 3|  = 2

  |2x + 3| = 2

If 2x + 3 ≥0, 2x ≥ -3 and x ≥ -3/2

If 2x + 3 < 0, 2x < -3 and x < -3/2

left ------------ -3/2 ----------- right
 
You can pick a number on the right of -3/2 or on the left of -3/2.

If you pick any number on the right of -3/2, 2x + 3 will be positive. For example, if you pick -1/2, 2(-1/2) + 3 = 2(-0.5) + 3 = -1 + 3 = 2.

Therefore, |2x + 3| = 2x + 3 

You need to solve 2x + 3 = 2

2x + 3 = 2

2x + 3 - 3 = 2 - 3

2x = -1

x = -1/2

If you pick any number on the left of -3/2, 2x + 3 will be negative. For example, if you pick -2, 2(-2) + 3 = -4 + 3 = -1.

Therefore, |2x + 3| = -(2x + 3) 

You need to solve -(2x + 3) = 2

-(2x + 3) = 2

2x + 3  = -2 

2x + 3 - 3 = - 2 - 3

2x = -5

x = -5/2

Solution = {-5/2, -1/2}

Solve tough absolute value equations: A complex case!

Example #2:  |2x + 6| + - 3 + |3x - 4| = 9

|2x + 6| + - 3 + 3 + |3x - 4| = 9 + 3

|2x + 6| + |3x - 4| = 12

This problem is complex because you have multiple cases to consider.

If 2x + 6 ≥ 0, 2x ≥ -6 and x ≥ -3

If 2x + 6 < 0, 2x < -6 and x < -3


If 3x - 4 ≥0, 3x ≥ 4 and x ≥ 4/3

If 3x - 4 < 0, 3x < 4 and x < 4/3

The number that we pick could be on the left of -3, between -3 and 4/3, or on the right of 4/3.

Left ---- -3 ---- between ---- 4/3 ---- right                               

On the left of -3, both 2x + 6 and 3x - 4 will be negative. For example, if x  = -4

2x + 6 = 2 times -4 + 6 = -8 + 6 = -2

3x - 4 = 3 times -4 - 4 = -12 - 4 = -16

Therefore, |2x + 6| = -(2x + 6) and |3x - 4| = -(3x - 4)

We need to solve -(2x + 6) + -(3x - 4) = 12


Multiply everything by -1


-1 times -(2x + 6) +  -1 times -(3x - 4) = -1 times 12


2x + 6 + 3x - 4 = -12

2x + 3x + 6 - 4 = -12


5x + 2 = -12

5x + 2 - 2 = -12 - 2

5x = -14

x = -14/5 = -2.8

This answer will make no sense since we chose our number on the left of -3. However, -2.8 is on the right of -3. So -2.8 will not solve the equation.

Between - 3 and 4/3,  2x + 6 is positive and 3x - 4 is negative. For example, if x  = -1

2x + 6 = 2 times -1 + 6 = -2 + 6 = 4

3x - 4 = 3 times -1 - 4 = -3 - 4 = -7

Therefore, |2x + 6| = (2x + 6) and |3x - 4| = -(3x - 4)

We need to solve (2x + 6) + -(3x - 4) = 12

2x + 6 + -3x + 4  = 12

2x + -3x + 6 + 4  = 12

-x + 10 = 12

-x + 10 - 10 = 12 - 10

-x  = 2

x = -2

-2 is between -3 and 4/3. Check the answer.

|2x + 6| + |3x - 4| = |2 × -2 + 6| + |3 × -2 - 4| = |-4 + 6| + |-6 - 4| = |2| + |-10| = 12

On the right of 4/3, both 2x + 6 and 3x - 4 will be positive. For example, if x  = 3

2x + 6 = 2 times 3 + 6 = 6 + 6 = 12

3x - 4 = 3 times 3 - 4 = 9 - 4 = 5

Therefore, |2x + 6| = 2x + 6 and |3x - 4| = 3x - 4

We need to solve (2x + 6) + (3x - 4) = 12

2x + 6 + 3x - 4  = 12

2x + 3x + 6 - 4  = 12

5x + 2  = 12

5x + 2 - 2 = 12 - 2

5x = 10

x = 10/5 = 2

2 is on the right of 4/3. Check the answer.

|2x + 6| + |3x - 4| = |2 × 2 + 6| + |3 × 2 - 4| = |4 + 6| + |6 - 4| = |10| + |2| = 12

Solution = { -2, 2}