Solving Proportions

Solving proportions by using cross product to find unknown terms is what this lesson is about. We will also show some principles, special techniques or shortcuts that can be used to quickly solve a proportion. Begin your study with the interactive lesson below. 

Interactive Proportion Solver

Terms to know:

Variables such as x, y, or any other letter are used to stand for an unknown number.

Unknown term: The missing or unknown number in a proportion.

We have seen in the lesson about proportions that we can use cross product to determine if the fractions or ratios are in proportions.

Cross products can also be used to find an unknown term in a proportion. Here is how!

Then, a × d = b × c

Examples Showing How to Use the Cross Products to Solve Proportions

Example #1:

Solve for x.

Since these two fractions or ratios are in proportions, we know that the cross product must be equal.

Using the cross product, we get:

5 × 16 = x × 10

80 = 10x

If you know your multiplication table you can quickly get the answer.

If 10 × x = 80, then x should be 8 because 10 × 8 is 80.

x = 8

Here is what the proportion becomes

Notice that 5 × 16 = 8 × 10 = 80

You can also break the problem down into more steps if you like as shown below:

The first cross product also called product of the extremes is:

5 × 16 = 80

The second cross product also called product of the means is:

10 × x

Setting the cross products equal, we get:

10 × x = 80

There is a faster way to get the answer when solving proportions. Look at the proportion again:

Example #2:

Solve for n.

Using the cross product, we get:

8 × 25 = 10 × n

200 = 10n

Instead of asking yourself " 10 times what equals 200? " we will this time solve the equation in order to show you another way to get n.

Divide both sides by 10

200/10 = 10n / 10

20 = n

Useful Equivalent Proportions You Can Use When Solving Proportions

Principle #1:

Then, 

Proof:

Add 1 to both sides of the equation and do the math as demonstrated:

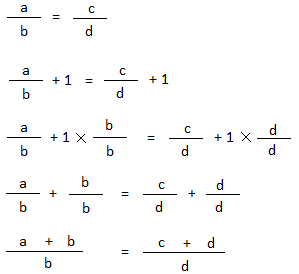
The above can be useful if you are solving the proportion below:

The proportion becomes 

The one immediately above is of course a lot easier to solve!

Principle #2:

Then, y = 4

For example, take a look at the following proportion

Then,  y = 100

Similarly if

x = 18

Principle #3:

Then, 

Proof:

Cross multiply:

b × c = a × d

bc = ad

Add ab to both sides of the equation

ab + bc = ab + ad

Factor b from the left side. Factor a from the right side.

b(a + c) = a(b + d)

Rewrite the above as a proportion. It is like undoing a cross multiplication.

Why is principle #3 useful when solving proportions? Say you need to solve the following proportion.

It is equivalent to

Again, the last format has a friendly look and it can be solved faster. Just remember these 3 principles when solving proportions and it will ease the proportion exercise for you. Thanks for reading!