Subtracting Integers
Interactive lesson for subtracting two integers on the number line
Rules for Subtracting Integers:
- Subtracting a positive number means moving left on the number line ⟵
- Subtracting a negative number means moving right on the number line ⟶
- Remember: Subtracting a negative is the same as adding a positive!
- Start at the first number, then move according to the second number
How to Subtract Integers
When subtracting integers, use a number line to help you think through problems. We illustrate with some examples below.
For example: 4 - 6
6 is positive, so 4 - 6 = 4 - (+6)
Here, you are subtracting a positive from a positive, so the result is less positive.
Therefore, you will start at 4 and you have to move to the left.
In this case, you will move 6 units to the left.
You end up at -2, so the answer is -2. Take a look at the number line below to see how this is done.

Find the answer to -5 ─ -6.
Before you do this problem, it is important to lay down some foundation.
In mathematics, whenever you subtract something from the same thing you get 0.
Mathematically speaking,
x - x = 0
7 - 7 = 0
15 - 15 = 0
Would it make sense then to say that -4 ─ -4 = 0?
Of course it would because you are subtracting negative 4 from negative 4.
Since the answer is 0 and you started at -4, you had to move to the right to end up at zero. This is crucial information I am giving you here!
In general, subtracting a negative from a negative makes the result less negative or more positive and you have to move to the right to get the answer. Where else can you get a deep understanding of math, if not right here?
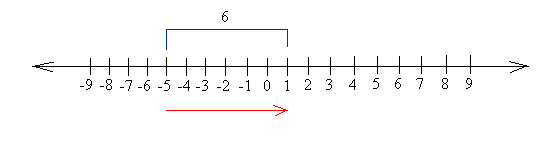
Having said that, to find -5 ─ -6, you have to start at -5 and move 6 units to the right.
If you do that, you will end up at 1, so the answer is 1.
If you subtract a negative from a positive, you will have to move to the right too. In fact, whenever you subtract a negative from anything, you have to move to the right for the same reason we explained above.
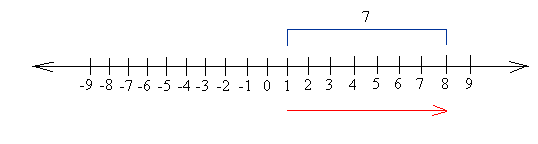
Find the answer to 1─ -7
Start at 1 and move 7 units to the right. You end up at 8, so the answer is 8.
In practice, it is convenient to change the minus sign and the negative sign next to it into an addition sign and a positive sign.
-2 ─ -3 = -2 + + 3 = 1
4 ─ -5 = 4 + + 5 = 9
Finally, subtracting a positive from a negative makes the result less positive, so you will move to the left to get the answer.
Find the answer to -1 ─ 8
Start at -1 and move 8 units to the left. You end up at -9, so the answer is -9.

Here is a summary for subtracting integers
4 ─ (+5) = 4 + (-5) = -1
-5 ─ (-6) = -5 + 6 = 1
5 ─ (-7) = 5 + (+7) = 12
-6 ─ (+8) = -6 + (-8) = -14
Here is the rule:
When subtracting integers, add the opposite.
3 ─ 5 = 3 + (-5) = -2
3 ─ -5 = 3 + +5 = 8
Other popular topics are modeling integers with chips and integers and inductive reasoning.