Tessellations in geometry
A couple of examples of tessellations in geometry are shown below. Basically, whenever you place a polygon together repeatedly without any gaps or overlaps, the resulting figure is a tessellation. A tessellation is also called tiling. Of course, tiles in your house is a real-life example of tessellation.
Tessellation with rectangles
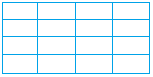
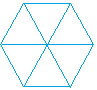
Tessellation with equilateral triangles
Tessellations in geometry: How to quickly check if a geometric figure will tessellate.
What makes the above figures tessellations?
1) The rectangles or triangles are repeated to cover a flat surface.
2) No gaps, or overlaps between the rectangles or the triangles.
Not all figures will form tessellations in geometry. When a figure can form a tessellation, the figure is said to tessellate.
Every triangle tessellates
Every quadrilateral tessellates
Why can we say with confidence that the above 2 statements are true?
Well, since there are no gaps and no overlaps, the sum of the measures of the angles around any vertex must be equal to 360 degrees as seen below with red circles.
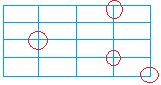
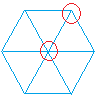
Therefore, if the measure of an angle of a figure is not a factor of 360, it will not tessellate. This is a very important concept since it will help determine when a figure can tessellate.
We can use then the formula to find the interior angle of a regular polygon to check if a figure will tessellate.
Interior angle of a regular polygon = [180 × (n-2)] / n
A couple of examples showing how to use the formula above to determine which figures will tessellate.
Example #1
Determine whether a regular pentagon will tessellate
A pentagon has 5 sides, so n = 5.
Interior angle of the pentagon = [180 × (5-2)] / 5
Interior angle of the pentagon = [180 × 3] / 5
Interior angle of the pentagon = 540 / 5
Interior angle of the pentagon = 108 degrees
There is no way to make 360 with 108 since 108 + 108 + 108 = 324 and 108 + 108 + 108 + 108 = 432
Therefore the pentagon will not tessellate as you can see below:
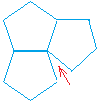
The gap is shown with a red arrow!
Example #2
Determine whether a regular hexagon will tessellate
A hexagon has 6 sides, so n = 6.
Interior angle of the hexagon = [180 × (6-2)] / 6
Interior angle of the hexagon = [180 × 4] / 6
Interior angle of the hexagon = 720 / 6
Interior angle of the hexagon = 120 degrees
120 is a factor of 360, so the hexagon will tessellate.
Example #3
Determine whether a regular 16-gon will tessellate
A 16-gon has 16 sides, so n = 16.
Interior angle of the 16-gon = [180 × (16-2)] / 16
Interior angle of the 16-gon = [180 × 14] / 16
Interior angle of the 16-gon = 2520 / 16
Interior angle of the 16-gon = 157.5 degrees
157.5 is not a factor of 360, so the 16-gon will not tessellate.
Tessellations can happen with translations, rotations, and reflections and it can also happen with irregular figures.
Types of tessellations
The most common types of tessellations are regular tessellations and semi-regular tessellations.
Regular tessellations
Regular tessellations are made using only regular polygons. For example, you can only use an equilateral triangle, a square, octagon, or any other regular polygon.
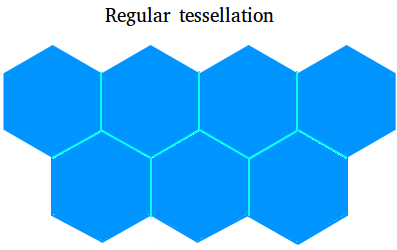
However, a regular tessellation can only be formed with an equilateral triangle, a square, and a hexagon.
If you use any other regular polygon, the interior angle of the regular polygon will never be a factor of 360. The following figure shows a regular tessellation made with hexagons.
Semi-regular tessellations
A semi-regular tessellation is put together with two or more regular polygons. The following semi-regular tessellation is made up of triangles and octagons.
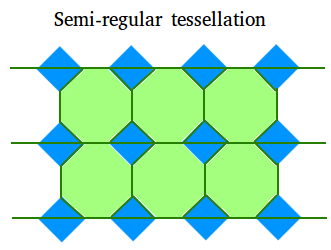
Eight types of semi-regular tessellations can be formed
- Using squares and octagons like the one shown above
- Using triangles and squares (two different patterns)
- Using hexagons and triangles (two different patterns)
- Using dodecagons and triangles
- Using dodecagons, squares, and hexagons
- Using hexagons, triangles, and squares