Transformations in math

Transformations in math occur when there is a change in position, shape, or size. When you are playing with a jigsaw puzzle, you could move a puzzle piece by sliding it, flipping it, or turning it.

Each of these moves is a transformation of the puzzle piece.

In a transformation, the original figure is a preimage and the resulting figure is an image.

A transformation is an isometry if the preimage and the image are congruent. Is the transformation below an isometry?

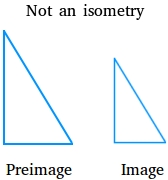
Since the transformation involves a change in size, it is not an isometry. The sides of the preimage triangle and the sides of the image triangle are not congruent or equal.

Types of transformations in math

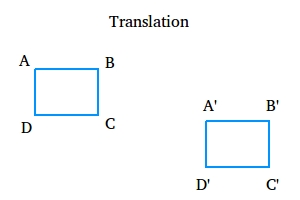
Translation

A translation or slide is an isometry in which all points of a figure move the same distance and in the same direction.

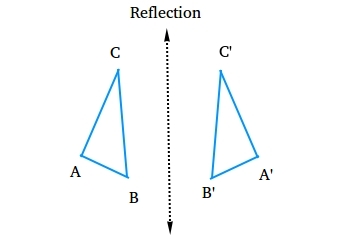
Reflection

A reflection is an isometry in which the preimage and the image have opposite orientations. In other words, the image appears backwards.

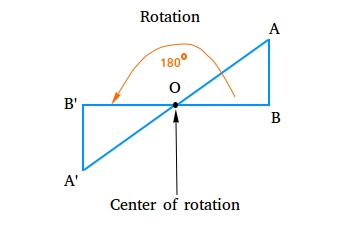
Rotation

A rotation is an isometry in which a figure has been rotated or turned around a point called center of rotation.

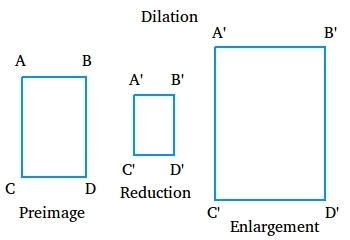
Dilation

A dilation is a transformation whose preimage and image are similar. In general, a dilation is not an isometry. A dilation could be an enlargement or a reduction.

Composition of transformation

A composition of transformation is a combination of two or more transformations. For example, a figure could be translated and then reflected. A figure could be reflected and then rotated. A figure could be translated, reflected, rotated, and dilated. It all depends on the problem and the situation.

Looking at this figure again, can you tell what kind of transformations were performed on the preimage?

The preimage was moved to the right and we can see that the image is smaller than the preimage. Therefore, the preimage was translated and dilated.

Transformations in math and the use of notation

A transformation maps a preimage onto its image and the symbol that we use to describe this mapping is an arrow pointing to the right(→)

To identify image points, we use the prime symbol ( ' )

A preimage point could be identified with A while the image point could be identified with A'.

The notation ∆ABC→∆A'B'C' means triangle ABC maps onto triangle A prime B prime C prime.