Triangular numbers

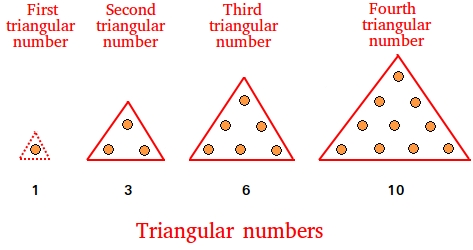
Triangular numbers are numbers that represent the shapes that you see below. My goal is to help you examine the pattern and derive a formula.

Looking at the pattern, you should see that the first 4 numbers are 1, 3, 6, and 10.
If we can find how many dots there are in the 100th triangular number, it will be fairly easy to derive a general formula.

Here is how to derive a formula that can help us find triangular numbers

Here is how to proceed:

First number: 1

Second number: 3 = 1 + 2

Third number: 6 = 1 + 2 + 3

Fourth number: 10 = 1 + 2 + 3 + 4

Hundredth number: ? = 1 + 2 + 3 + 4 + 5 + 6 +....+ 100

Instead of adding in that order, you can add as shown below (credited to Gauss)

(1 + 100) + (2 + 99) + (3 + 98) + (4 + 97) + ......+ (50 + 51)

Notice that each pair is equal to 101. Furthermore, since we are pairing the numbers, and there are 100 numbers, there will be 50 pairs.

Therefore, instead of adding 101 fifty times, you can just multiply 101 by 50

Since 50 × 101 = 5050, the sum for 1 + 2 + 3 + 4 + 5 + 6 +....+ 100 is equal to 5050

You can play with 50 × 101 to get a general formula.

If we can rewrite 50 × 101 and make 100 appear into the expression, we can just make a prediction and say that 100 represents the hundredth number.

Then, we can simply replace 100 by n and n will represent the nth number.

It is not a complete proof. You just make a sound and logical conclusion based on a pattern.

50 × 101 = (100/2) × 101 = (100/2) × (100 + 1)

If we substitute 100 for n, the formula we get is (n/2) × (n + 1)

Now let's test the formula for the first 4 numbers above

First number: (1/2) × (1 + 1) = (1/2) × 2 = 1

Second number: (2/2) × (2 + 1)= 1 × (2 + 1) = 1 × 3 = 3

Third number: (3/2) × (3 + 1) = 3/2 × 4 = 12/2 = 6

Fourth number: (4/2) × (4 + 1) = 4/2 × 5 = 2 × 5 = 10

Since the formula is working for 5 numbers, you have a pattern and it is reasonable to conclude that it will work for all triangular numbers