Venn diagram word problems
The Venn diagram word problems in this lesson will show you how to use Venn diagrams with 2 circles to solve problems involving counting.
Venn diagram word problems with two circles
Word problem #1
A survey was conducted in a neighborhood with 128 families. The survey revealed the following information.
- 106 of the families have a credit card
- 73 of the families are trying to pay off a car loan
- 61 of the families have both a credit card and a car loan
Answer the following questions:
1. How many families have only a credit card?
2. How many families have only a car loan?
3. How many families have neither a credit card nor a car loan?
4. How many families do not have a credit card?
5. How many families do not have a car loan?
6. How many families have a credit card or a car loan?
- Let C be families with a credit card
- Let L be families with a car loan
- Let S be the total number of families
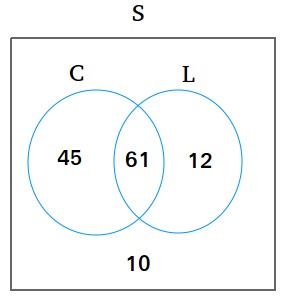
The Venn diagram above can be used to answer all these questions.
Tips on how to create the Venn diagram.
Always put first, in the middle or in the intersection, the value that is in both sets. For example, since 61 families have both a credit card and a car loan, put 61 in the intersection before you do anything else.
In C only, put 45 since 106 - 61 = 45
In L only, put 12 since 73 - 61 = 12
Outside C and L, put 10 since 128 - 61 - 45 - 12 = 10
Solution
The expression, "only a credit card" means that it is only in C. Any number in L cannot be included.
1. The number of families with only a credit card is 45. Do not add 61 to 45 since 61 is in L.
2. The number of families with only a car loan is 12.
3. The number of families with neither a credit card nor a car loan is 10. 10 is not in C nor in L.
4. The number families without a credit card is found by adding everything that is not in C.
12 + 10 = 22
5. The number families without a car loan is found by adding everything that is not in L.
45 + 10 = 55
6. The number of families with a credit card or a car loan is found by adding anything in C only, in L only and in the intersection of C and L?
45 + 61 + 12 = 118
Word problem #2
A survey conducted in a school with 150 students revealed the following information:
- 78 students are enrolled in swimming class
- 85 students are enrolled in basketball class
- 25 are enrolled in both swimming and basketball class
Answer the following questions:
1. How many students are enrolled only in swimming class?
2. How many students are enrolled only in basketball class?
3. How many students are neither enrolled in swimming class nor basketball class?
4. How many students are not enrolled in swimming class?
5. How many students are not enrolled in basketball class?
6. How many students are enrolled in swimming class or basketball class?
- Let S be students enrolled in swimming class
- Let B be students enrolled in basketball class
- Let E be the total number of students
Using the same technique as in problem #1, we have the following Venn diagram
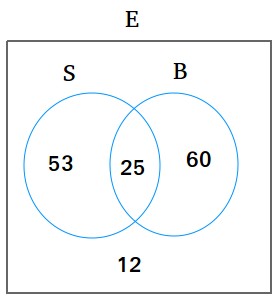
1. The number of students enrolled only in swimming class is 53
2. The number of students enrolled only in basketball class is 60
3. The number of students who are neither enrolled in swimming class nor basketball class is 12
4. Students not enrolled in swimming class are enrolled in basketball class only or are enrolled in neither of these two activities. In other words, everything that is not in S.
60 + 12 = 72
5. Students not enrolled in basketball class are enrolled in swimming class only or are enrolled in neither of these two activities. In other words, everything that is not in B.
53 + 12 = 65
6. The number of students enrolled in swimming class or basketball class is found by adding anything in S only, in B only and in the intersection of S and B?
53 + 25 + 60 = 138
A tricky Venn diagram word problem with two circles
Word problem #3
In a survey of 100 people, 28 people smoke, 65 people drink, and 30 people do neither. How many people do both?
Solution
- Let K be the number of people who smoke
- Let D be the number of people who drink
- Let E be the total number of people
- Let x be the number of people who smoke and drink
If we make a Venn diagram, here is what we have so far.
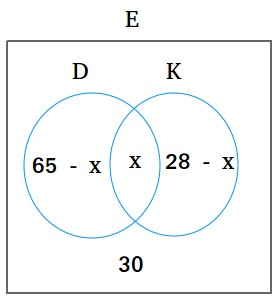
We end up with the following equation to solve for x.
(65 - x) + x + (28 - x) + 30 = 100
65 - x + x + 28 - x + 30 - 30 = 100 - 30
65 - x + x + 28 - x = 70
65 + 0 + 28 - x = 70
93 - x = 70
Since 93 - 23 = 70, x = 23
The number of people who do both is 23.