Volume of a sphere
The volume of a sphere is how much space the sphere occupies. In the figure below, notice that the sphere on the left occupies less space than the sphere on the right. Therefore, the sphere on the left has less volume.
Volume of a sphere formula
Given the radius, the volume can be found by using the following formula:
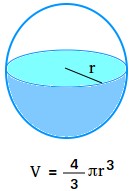
V = (4/3)pir3 = (4/3)πr3
pi or π is a special mathematical constant, and it is approximately equal to 22/7 or 3.14.
If r or the radius of the sphere is known, the volume is four thirds the product of pi and the cube of the radius of the sphere.
Suppose the diameter is given instead of the radius. Since the radius is half of the diameter, just divide the diameter by 2 to get the radius before looking for the volume.
If you must use the diameter, V = (4/3)π(d/2)3 = (4/3)π(d3/8) = 4πd3/24 = πd3/6
The volume is expressed in cubic units.
- If r is measured in meters, then the volume is measured in cubic meters or m3.
- If r is measured in centimeters, then the volume is measured in cubic centimeters or cm3.
- If r is measured in inches, then the volume is measured in cubic inches or in.3
Some examples showing how to get the volume of a sphere
Example #1
Find the volume of a sphere that has a radius of 2 inches
Volume = 4/3 × π × r3
Volume = 4/3 × 3.14 × 23
Volume = 4/3 × 3.14 × 8
Volume = 4/3 × 25.12
Volume = 4/3 × 25.12 / 1
Volume = (4 × 25.12)/(3 × 1)
Volume = (100.48) / 3
Volume = 33.49 cubic inch = 33.49 in.3
Find the volume of a sphere with a radius of 3 feet
Volume = 4/3 × π × r3
Volume = 4/3 × 3.14 × 33
Volume = 4/3 × 3.14 × 27
Volume = 4/3 × 84.78
Volume = 4/3 × 84.78/1
Volume = (4 × 84.78)/(3 × 1)
Volume = (339.12)/3
Volume = 113.04 ft3 = 113.04 cubic feet
Example #3
Find the volume of a sphere of radius 2/3 cm
Volume = 4/3 × π × r3
Volume = 4/3 × 3.14 × (2/3)3
Volume = 4/3 × 3.14 × 2/3 ×2/3 × 2/3
Volume = 4/3 × 3.14 × 8/27
Volume = 4/3 × 3.14/1 × 8/27
Volume = (4 × 3.14 × 8) / ( 3 × 1 × 27 )
Volume = (100.48)/(81)
Volume = 1.24 in.3
Volume of a hollow sphere
Suppose a sphere with an inner radius r is removed from a sphere with an outer radius R. What you end up with is called a hollow sphere or a sphere that has a cavity inside of it. In the figure below, the cavity is shown in red.
The volume of the cavity is the volume of the sphere that is removed.
The volume of the hollow sphere is whatever is left after the volume of the cavity is removed. This is shown with the aquamarine color.
Volume of the hollow sphere = volume of the whole sphere - volume of the cavity.
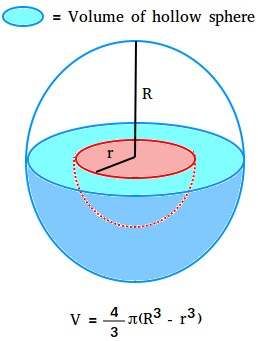
Volume of hollow sphere = (4/3)πR3 - (4/3)πr3
Factor out (4/3)π
Volume of hollow sphere = (4/3)π(R3 - r3)
Volume of a hemisphere
A hemisphere is half a sphere. To find the volume of a hemisphere, just divide the formula to find the volume by 2.
V = [(4/3)πr3]/2
V = (2/3)πr3
The volume of a hemisphere is two thirds the product of pi and the cube of the radius of the sphere.
Volume of a sphere using the circumference of a sphere
C = 2πr
V = (4/3)πr3
r = C/2π
V = (4/3)π(C/2π)3
V = (4/3)π(C3/8π3)
V = (4πC3)/(24π3)
V = (4πC3)/(4π)(6π2)
Cancel 4π
V = (C3)/(6π2)
What is the volume of the earth?
The earth is a sphere with a radius of 6356 kilometers or 3958.8 miles. What is the volume of the earth in cubic miles?
Volume of the earth = 4/3 × π × 3958.83Volume of the earth = 4/3 × 3.14 × 3958.8 ×3958.8 × 3958.8
Volume of the earth = 4/3 × 3.14 × 62042699345.5
Volume of the earth = 4/3 × 194814075945
Volume of the earth = 4/3 × 194814075945/1
Volume of the earth = (4 × 194814075945)/(3 × 1)
Volume of the earth = (779256303779)/(3)
Volume of the earth = 259,752,101,260 cubic miles
The earth has approximately a volume of 260 trillion cubic miles.
Derivation of the volume of a sphere
We need calculus, especially the concept of integration, in order to derive the volume of a sphere or to show you a proof. Take a look at the sphere below and study it carefully!
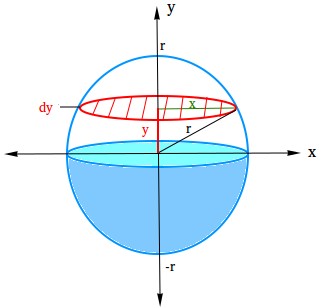
- The red circle is a thin disc. Think of it as a very flat cylinder!
- x is the radius of the thin disc
- dy is the thickness of the thin disc
- r is the radius of the sphere
- y is the distance from the x-axis to the disc.
Using the Pythagorean theorem, r2 = x2 + y2
x2 = r2 - y2
The volume of the thin disc at that specific height is πx2dy
Substitute r2 - y2 for x2 in πx2dy
V = π(r2 - y2)dy
The total volume of the sphere is found by adding the volumes of all disks for all possible heights you can put those disks inside the sphere.
All the possible heights are between -r and r (-r ≤ y ≤ r)
The sign that you see bellow is the integral symbol and it a summation, meaning to add everything.
$$ \int_{}^{} $$The one below means to add everything from -r ro r
$$ \int_{-r}^{r} $$The one below means to add together the volumes of all disks for all possible heights you can put those disks (-r ≤ y ≤ r).
$$ \int_{-r}^{r} π(r^2 - y^2) \,dy $$According to linearity rule, you can move pi outside the integral sign.
$$ π \int_{-r}^{r} (r^2 - y^2) \,dy $$ $$ π \int_{-r}^{r} (r^2 - y^2) \,dy = π[yr^2 - \frac {y^3}{3} ]_{-r}^ {r} $$ $$ π \int_{-r}^{r} (r^2 - y^2) \,dy = π[(r^3 - \frac {r^3}{3} - (-r^3 - \frac {-r^3}{3} )] $$ $$ π \int_{-r}^{r} (r^2 - y^2) \,dy = π[( \frac {2r^3}{3} - ( \frac {-2r^3}{3} )] $$ $$ π \int_{-r}^{r} (r^2 - y^2) \,dy = π[( \frac {2r^3}{3} + ( \frac {2r^3}{3} )] $$ $$ π \int_{-r}^{r} (r^2 - y^2) \,dy = π( \frac {4r^3}{3}) $$ $$ π \int_{-r}^{r} (r^2 - y^2) \,dy = (\frac{4}{3}πr^3) $$