Word problems involving quadratic equations

Check out these four great word problems involving quadratic equations in this lesson. 

Problem #1: A rectangular garden has an area of 14 m² and a perimeter of 18 meters. Find the dimensions of the rectangular garden. The figure below shows how to set up the problem.

Solution:

Let w = width and l = length

2l + 2w = 18

lw = 14

Divide both sides of 2l + 2w = 18 by 2 to get l + w = 9.

Using l + w = 9, solve for l. We get l = 9 - w.

Substitute 9 - w for l in lw = 14

( 9 - w)w = 14  
9w - w² = 14
9w - w² - 14 = 0
- w² + 9w - 14 = 0
w² - 9w + 14 = 0

(w - 7)(w - 2) = 0

w = 7 and w  = 2

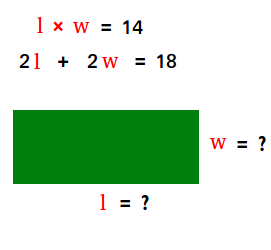
Problem #2: The sum of two numbers is 12 and their product is 35. What are the two numbers?

Solution: 

Let n and m be the two numbers.

n + m = 12  (1)
n × m = 35  (2)

Using (1), n = 12 - m

(12 - m) × m = 35

12m - m² = 35

- m² + 12m - 35 = 0

m² + -12m + 35 = 0

(m - 5)(m - 7) = 0

m = 5 and m = 7. The two numbers are 5 and 7

Interesting word problems involving quadratic equations.

Problem #3: The quadratic equation for the cost in dollars of producing automobile tires is given below where x is the number of tires the company produces. Find the number of tires that will minimize the cost.

C = 0.00002x² - 0.04x + 38

Solution: 

The standard form of a quadratic equation is ax² + bx + c. To solve this problem, we just need 2 important concepts about quadratic equations. First, when we are trying to maximize or minimize, we need to use the formula below that will help us find the x-coordinate of the vertex. Second, if a > 0, the vertex is a minimum. if a < 0, the vertex is a maximum.

To minimize the cost, the company should produce 1000 tires.

Problem #4: You want to frame a collage of pictures with a 9-ft strip of wood. What dimensions will help you maximize the area?


Solution: 

First, we need to find the quadratic equation. 

Area = l × w                                   Perimeter = 2l + 2w

9 = 2l + 2w. Solve for l and replace l in the formula for the area.

9 - 2w = 2l

A = -w² + 4.5w

A = -w² + 4.5w + 0

To maximize the area, l = w = 2.25

If you found the word problems involving quadratic equations on this lesson difficult to understand, review the lesson about factoring trinomials