Work word problems in physics
These work word problems will show how to calculate the work when the
force applied to the object and the displacement of the object
are known. You will therefore use the formula w = F × d
Problem #1:
How many joules of work are done against a cart when a force of 50 N pushes it 1 kilometer away?
Solution:
First convert 1 kilometer to meter. 1 kilometer = 100 meters.
Then, use the formula w = F × dw = 50 N × 100 meters
w = 5000 N.m
w = 5000 joules
Interesting work word problems
Problem #2:
Work of 2000 J is required to push an object.
1) Give 2 examples of what F and d could be.
2) How much work is required to lift the same object if the distance pushed is 3 times bigger?
3) How much work is required if the force is doubled?
Solution
1) Examples of what F and d could be
F = 200 N and d = 10 meters
F = 20 N and d = 100 meters
F = 50 N and d = 40 meters
2) Pick F = 50 N and d = 40 meters.
If the distance is 3 times bigger, d = 3 times 40 = 120 meters
W = 50 N × 120 m = 6000 JoulesWhen the distance is tripled, the work is also tripled
3) Pick F = 200 N and d = 10 meters
If F is 2 times bigger, F = 2 times 200 = 400
W = 400 N × 10 m = 4000 JoulesWhen the force is doubled, the work is also doubled
Problem #3:
In a tug of war, team x pulled team y with a force of 10000 N a distance of 50 meters. Team y did not win because they were only able to exert of force of 8000 N. Calculate the work of each team.
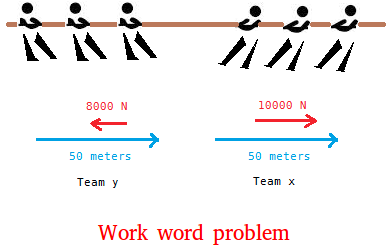
The graph above shows the force and direction for both teams.
For team x, the angle between the force and the direction is 0 degrees.
w = 10000 × 50 × cos(0)
{ cos(0) = 1
w = 10000 × 50 × 1
w = 500000 joules
For team y, the angle between the force and the direction is 180 degrees.
w = 10000 × 50 × cos(180)
{ cos(180) = -1
w = 8000 × 50 × -1
w = -400000 joules
Notice that the work is negative for team y.
This is going to be the case when the direction of the force is opposite to the direction of movement.